How to solve Leetcode 1679. Max Number of K-Sum Pairs

Problem statement

You are given an integer array nums and an integer k.

In one operation, you can pick two numbers from the array whose sum equals k and remove them from the array.

Return the maximum number of operations you can perform on the array.

Example 1

Input: nums = [1,2,3,4], k = 5
Output: 2
Explanation: Starting with nums = [1,2,3,4]:
- Remove numbers 1 and 4, then nums = [2,3]
- Remove numbers 2 and 3, then nums = []
There are no more pairs that sum up to 5, hence a total of 2 operations.

Example 2

Input: nums = [3,1,3,4,3], k = 6
Output: 1
Explanation: Starting with nums = [3,1,3,4,3]:
- Remove the first two 3's, then nums = [1,4,3]
There are no more pairs that sum up to 6, hence a total of 1 operation.

Constraints

• 1 <= nums.length <= 10^5.

• 1 <= nums[i] <= 10^9.

• 1 <= k <= 10^9.

Solution: Count the appearances

You can use a map to count the appearances of the elements of nums.

Example 2

For nums = [3,1,3,4,3] and k = 6:

• Initialize count = 0.

• For i = 0: m[3] = 1; k - 3 = 3 but m[3] is only 1, not enough to have two numbers.

• For i = 1: m[1] = 1; k - 1 = 5 and m[5] = 0.

• For i = 2: m[3] = 2; k - 3 = 3 and m[3] = 2 just enough to have two numbers to perform the sum. count = 1. Erase those two values 3's from the map: m[3] = 0.

• For i = 3: m[4] = 1; k - 4 = 2 and m[2] = 0.

• For i = 4: m[3] = 1; k - 3 = 3 but m[3] is only 1, not enough to have two numbers.

• Final count = 1.

Code

#include <vector>
#include <iostream>
#include <unordered_map>
using namespace std;
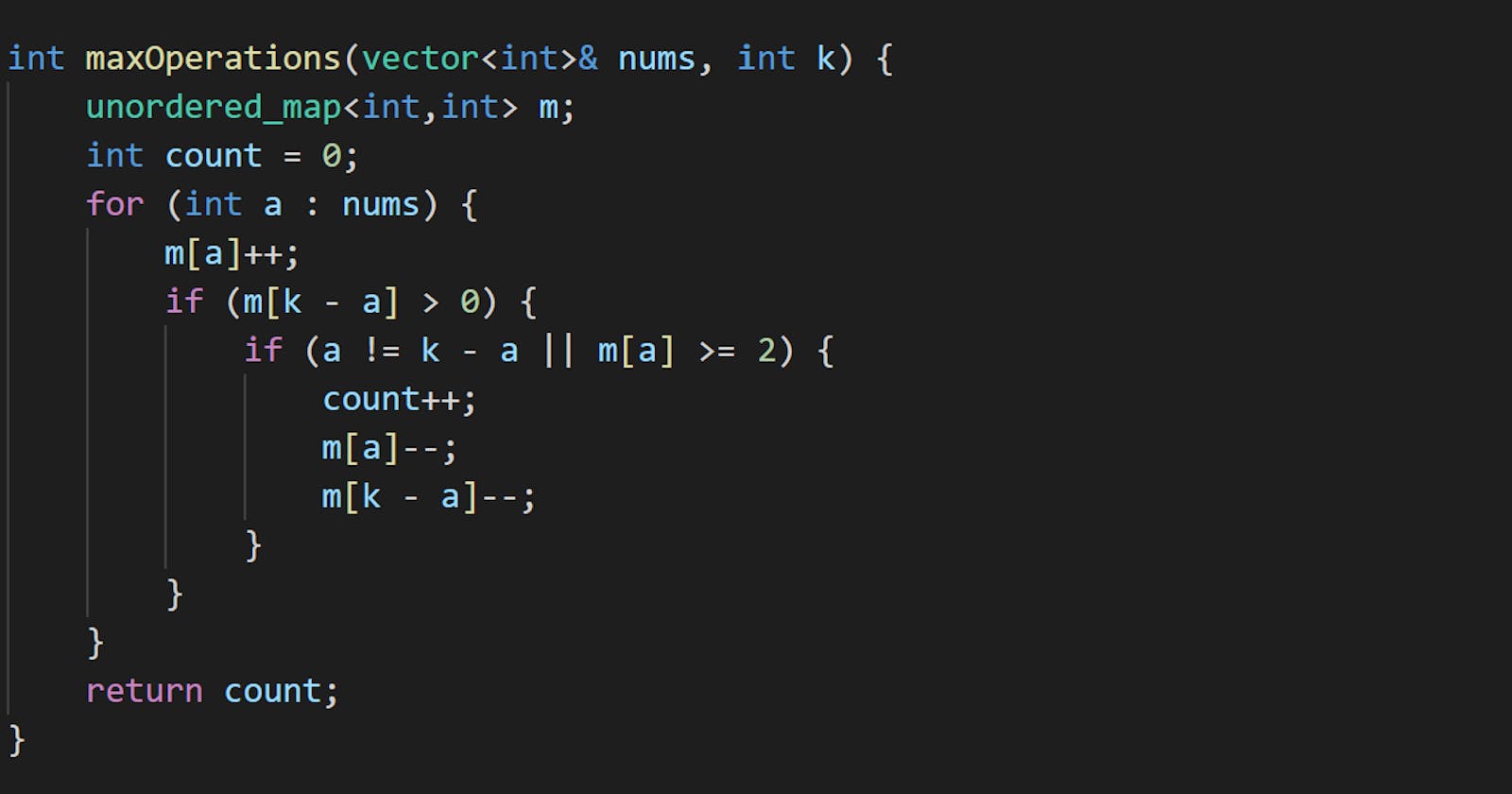
int maxOperations(vector<int>& nums, int k) {
    unordered_map<int,int> m;
    int count = 0;
    for (int a : nums) {
        m[a]++;
        if (m[k - a] > 0) {
            if (a != k - a || m[a] >= 2) {
                count++;
                m[a]--;
                m[k - a]--;
            }
        }
    }
    return count;
}
int main() {
    vector<int> nums{1,2,3,4};
    cout << maxOperations(nums, 5) << endl;
    nums = {3,1,3,4,3};
    cout << maxOperations(nums, 6) << endl;
}

Output:
2
1

Complexity

• Runtime: O(N), where N = nums.length.

• Extra space: O(N).

References

• https://leetcode.com/problems/max-number-of-k-sum-pairs/

• https://www.leetsolve.com/1679-max-number-of-k-sum-pairs

Get my FREE book "10 Classic Coding Challenges"