Problem statement

You are given a sorted array consisting of only integers where every element appears exactly twice, except for one element which appears exactly once.

Return the single element that appears only once.

Your solution must run in O(log n) time and O(1) space.

Example 1

Input: nums = [1,1,2,3,3,4,4,8,8]
Output: 2

Example 2

Input: nums = [3,3,7,7,10,11,11]
Output: 10

Constraints

• 1 <= nums.length <= 10^5.

• 0 <= nums[i] <= 10^5.

Solution 1: Bruteforce

Code

#include <vector>
#include <iostream>
using namespace std;
int singleNonDuplicate(vector<int>& nums) {
    for (int i = 0; i < nums.size() - 1; i += 2) {
        if (nums[i] != nums[i + 1]) {
            return nums[i];
        }
    }
    return nums[0];
}
int  main() {
    vector<int> nums{1,1,2,3,3,4,4,8,8};
    cout << singleNonDuplicate(nums) << endl;
    nums = {3,3,7,7,10,11,11};
    cout << singleNonDuplicate(nums) << endl;
    nums = {3};
    cout << singleNonDuplicate(nums) << endl;
}

Output:
2
10
3

Complexity

• Runtime O(n/2), where n = nums.length.

• Memory O(1).

Solution 2: Binary search

Since nums is sorted, you can perform a binary search on it.

Let us divide nums into two halves.

If the single element belongs to the right half, all elements of the left half satisfy nums[2*i] == nums[2*i + 1].

Conversely, if the single element belongs to the left half, that condition is violated at the middle element of nums (the middle one with an even index).

Example 1

For nums = [1,1,2,3,3,4,4,8,8]:

• The middle element with even index is nums[4] = 3. It is not equal to nums[4 + 1] = 4. So the single element must be somewhere in the left half [1,1,2,3,3].

• The middle element of nums = [1,1,2,3,3] with even index is nums[2] = 2, which is not equal to nums[2 + 1] = 3. So the single element must be somewhere in the left half [1,1,2].

• The middle element of nums = [1,1,2] with even index is nums[0] = 1 == nums[0 + 1]. So the single element must be somewhere in the right half [2].

• nums = [2] contains only one element. So 2 is the result.

Code

#include <vector>
#include <iostream>
using namespace std;
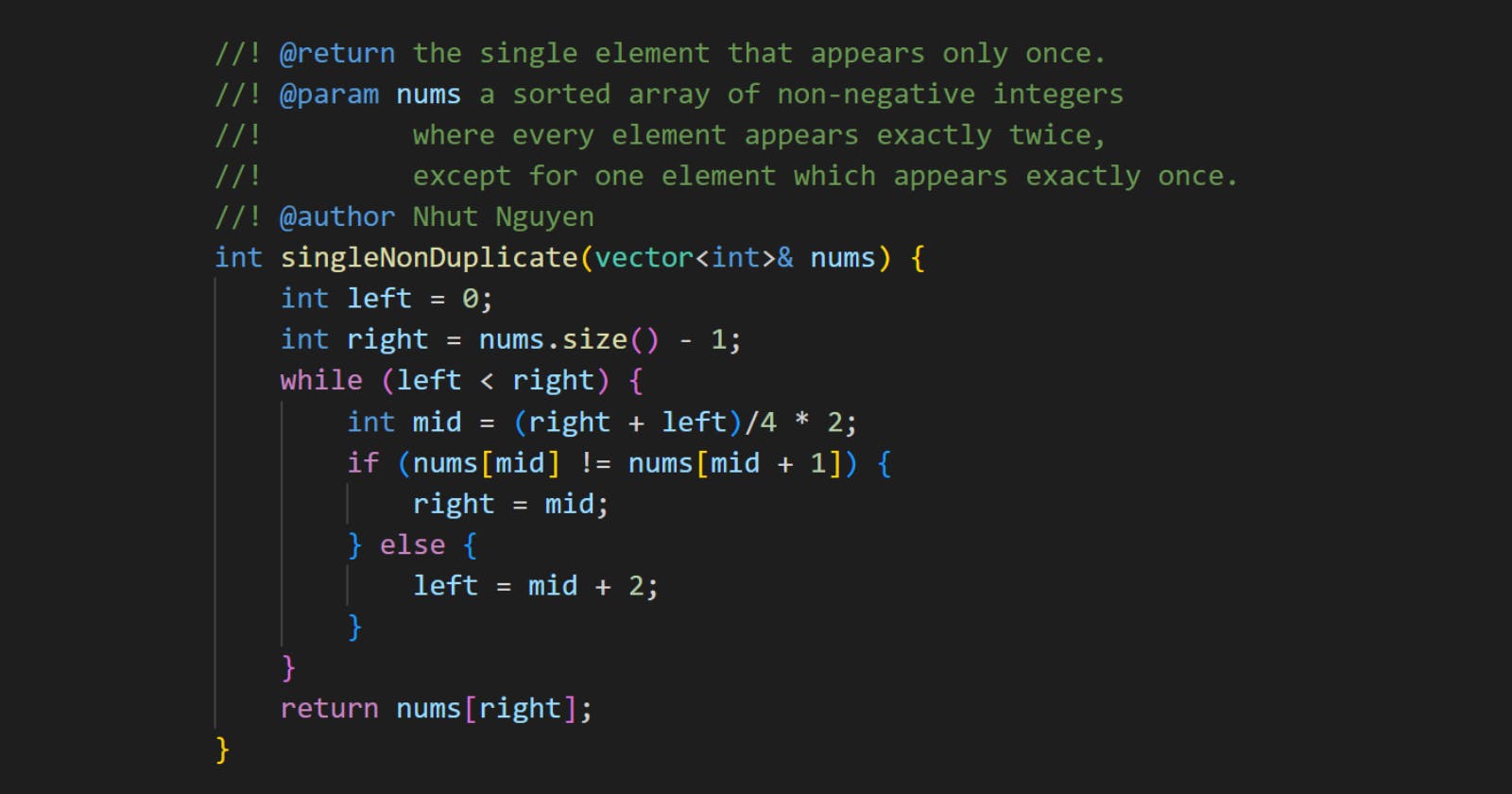
int singleNonDuplicate(vector<int>& nums) {
    int left = 0;
    int right = nums.size() - 1;
    while (left < right) {
        int mid = (right + left)/4 * 2; // to make sure mid is even
        if (nums[mid] != nums[mid + 1]) {
            right = mid;
        } else {
            left = mid + 2;
        }
    }
    return nums[right];
}
int  main() {
    vector<int> nums{1,1,2,3,3,4,4,8,8};
    cout << singleNonDuplicate(nums) << endl;
    nums = {3,3,7,7,10,11,11};
    cout << singleNonDuplicate(nums) << endl;
    nums = {3};
    cout << singleNonDuplicate(nums) << endl;
}

Output:
2
10
3

Complexity

• Runtime O(logn), where n = nums.length.

• Memory O(1).

Reference

• https://leetcode.com/problems/single-element-in-a-sorted-array/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.