Problem statement

Given an integer n, return the least number of perfect square numbers that sum to n.

A perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 1, 4, 9, and 16 are perfect squares while 3 and 11 are not.

Example 1

Input: n = 9
Output: 1
Explanation: 9 is already a perfect square.

Example 2

Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.

Example 3

Input: n = 7
Output: 4
Explanation: 7 = 4 + 1 + 1 + 1.

Example 4

Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.

Constraints

• 1 <= n <= 10^4.

Solution 1: Dynamic Programming

Let us call the function to be computed numSquares(n), which calculates the least number of perfect squares that sum to n.

Here are the findings.

1. If n is already a perfect square then numSquares(n) = 1.

2. Otherwise, it could be written as n = 1 + (n-1), or n = 4 + (n-4), or n = 9 + (n-9), etc. which means n is a sum of a perfect square (1, 4 or 9, etc.) and another number m < n. That leads to the problems numSquares(m) of smaller values m.

3. If you have gotten the results of the smaller problems numSquares(n-1), numSquares(n-4), numSquares(n-9), etc. then numSquares(n) = 1 + the minimum of those results.

Example 4

n = 12 is not a perfect square. It can be written as n = 1 + 11 = 4 + 8 = 9 + 3.

• For m = 11, it is not a perfect square and can be written as m = 1 + 10 = 4 + 7 = 9 + 2.

• For m = 8, it is not a perfect square and can be written as m = 1 + 7 = 4 + 4 (matched). You get numSquares(8) = 2.

• For m = 3, it is not a perfect square and can be written as m = 1 + 2.

You can continue to compute numSquares(m) for other values m in this recursive process. But you can see the case of m = 8 was already the best solution. And numSquares(12) = 1 + numSquares(8) = 1 + 2 = 3, which is the case of n = 12 = 4 + 4 + 4.

To improve runtime, you can apply dynamic programming to cache the numSquares(n) that you have computed.

Code

#include <iostream>
#include <cmath>
#include <unordered_map>
using namespace std;
int nsq(int n, unordered_map<int, int>& ns) {
    auto it = ns.find(n);
    if (it != ns.end()) {
        return it->second;
    }
    const int sq = sqrt(n);
    if (sq * sq == n) {
        ns[n] = 1;
        return 1;
    }
    int result = n;
    for (int i = 1; i <= sq; i++) {
        result = min(result, nsq(n - i*i, ns));
    }
    ns[n] = result + 1;
    return ns[n];
}
int numSquares(int n) {
    unordered_map<int, int> ns;
    return nsq(n, ns);
}
int main() {
    cout << numSquares(12) << endl;
    cout << numSquares(13) << endl;
}

Output:
3
2

Complexity

• Runtime: O(n^2).

• Extra space: O(n)

Solution 2: Number Theory

The dynamic programming solution above is good enough. But for those who are interested in Algorithmic Number Theory, there is a very interesting theorem that can solve the problem directly without recursion.

It is called Lagrange's Four-Square Theorem, which states

every natural number can be represented as the sum of four integer squares.

It was proven by Lagrange in 1770.

Example 4

n = 12 = 4 + 4 + 4 + 0 or 12 = 1 + 1 + 1 + 9.

Applying to our problem, numSquares(n) can only be 1, 2, 3, or 4. Not more.

It turns into the problem of

identifying when numSquares(n) returns 1, 2, 3, or 4.

Here are the cases.

1. If n is a perfect square, numSquares(n) = 1.

2. There is another theorem, Legendre's Three-Square Theorem, which states that numSquares(n) cannot be 1, 2, or 3 if n can be expressed as

    n = 4^a(8*b + 7),
   

   where a, b are nonnegative integers. In other words, numSquares(n) = 4 if n is of this form.

Example 3

n = 7 = 4^0(8*0 + 7). It can only be written as 7 = 4 + 1 + 1 + 1.

Code

#include <iostream>
#include <cmath>
using namespace std;
bool isSquare(int n) {
    int sq = sqrt(n);
    return sq * sq == n;
}
int numSquares(int n) {
    if (isSquare(n)) {
        return 1;
    }
    // Legendre's three-square theorem
    int m = n;
    while (m % 4 == 0) {
        m /= 4;
    }
    if (m % 8 == 7) {
        return 4;
    }
    const int sq = sqrt(n);
    for (int i = 1; i <= sq; i++) {
        if (isSquare(n - i*i)) {
            return 2;
        }
    }
    return 3;
}
int main() {
    cout << numSquares(12) << endl;
    cout << numSquares(13) << endl;
}

Output:
3
2

Complexity

• Runtime: O(logn).

• Extra space: O(1).

Solution 3: Further performance improvement

Lagrange's Four-Square Theorem and Legendre's Three-Square Theorem are so powerful to solve this problem. But you can still do a little more algebra to improve further the runtime of the implementation above.

Instead of looping over sqrt(n) in the final for loop, we will prove that this loop over sqrt(m) is enough. That will improve runtime a lot since m is much less than n.

Let m be the reduced value of n after the Legendre's while loop. It satisfies

n = 4^a * m.

We will prove that numSquares(n) = numSquares(m).

In fact, if m is written as m = x^2 + y^2 + z^2, where x, y, z are nonnegative integers. Then

n = 4^a * m = (2^a)^2 * m = (2^a * x)^2 + (2^a * y)^2 + (2^a * z)^2.

In other words, numSquares(n) = numSquares(m).

Now you can change directly the value n during the Legendre's while loop without affecting the final result.

Code

#include <iostream>
#include <cmath>
using namespace std;
bool isSquare(int n) {
    int sq = sqrt(n);
    return sq * sq == n;
}
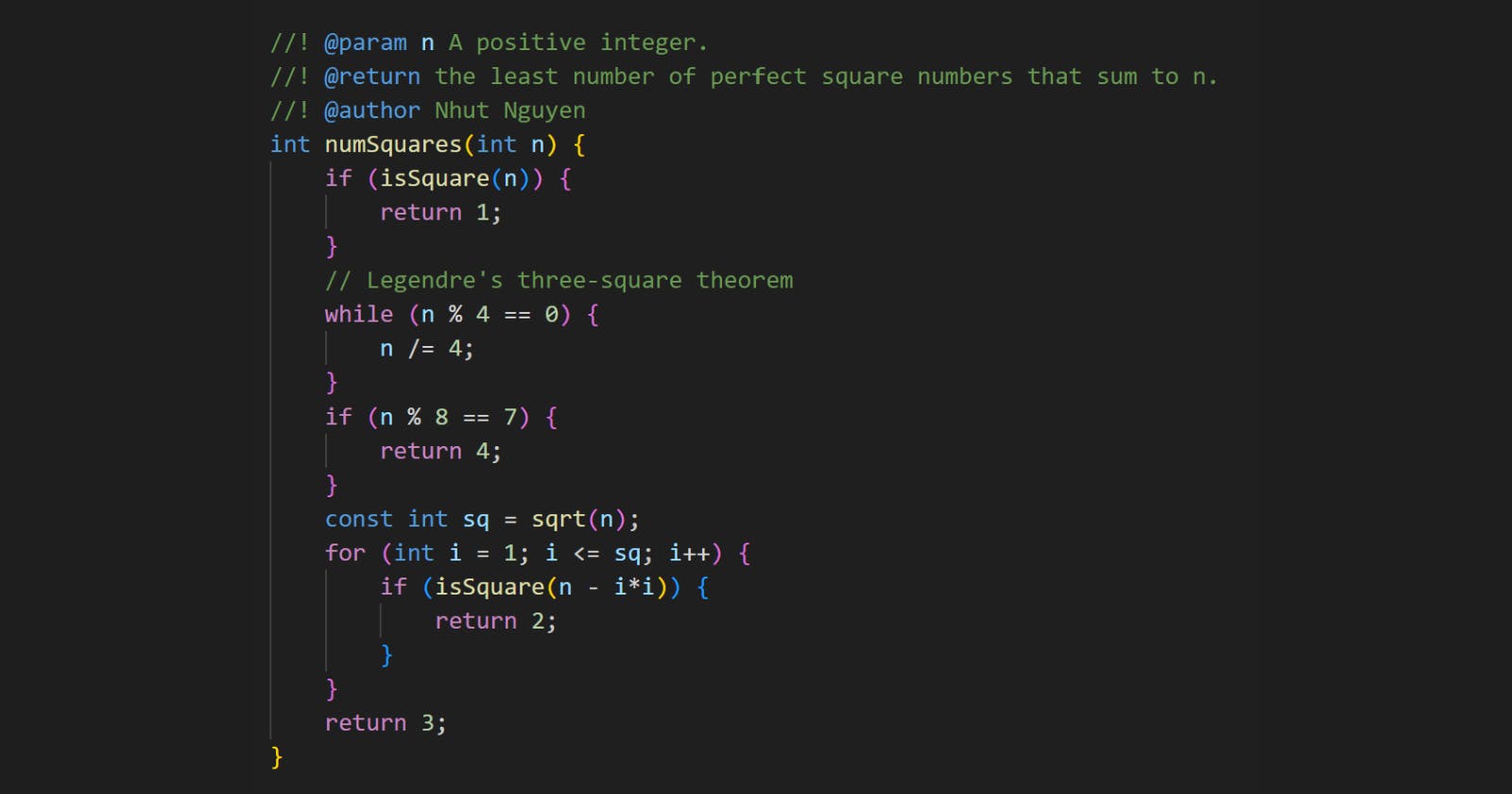
int numSquares(int n) {
    if (isSquare(n)) {
        return 1;
    }
    // Legendre's three-square theorem
    while (n % 4 == 0) {
        n /= 4;
    }
    if (n % 8 == 7) {
        return 4;
    }
    const int sq = sqrt(n);
    for (int i = 1; i <= sq; i++) {
        if (isSquare(n - i*i)) {
            return 2;
        }
    }
    return 3;
}
int main() {
    cout << numSquares(12) << endl;
    cout << numSquares(13) << endl;
}

Output:
3
2

Complexity

• Runtime: O(logn).

• Extra space: O(1).

Conclusion

• The title of this coding challenge (Perfect squares) gives you a hint it is more about mathematics than coding technique.

• It is amazing from Lagrange's Four-Square Theorem there are only four possibilities for the answer to the problem. Not many people knowing it.

• You can get an optimal solution to a coding problem when you know something about the mathematics behind it.

Hope you learn something from this code challenge.

Have fun with coding and mathematics!

---

Thanks for reading. Feel free to share your thought about my content and check out my FREE book 10 Classic Coding Challenges.

What is your approach? The problem was picked from leetcode.com. You can submit your solution in any programming language and check the performance.