Problem statement

You are given an array prices where prices[i] is the price of a given stock on the i-th day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

Example 1

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

Example 2

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.

Constraints

• 1 <= prices.length <= 10^5.

• 0 <= prices[i] <= 10^4.

Solution 1: Bruteforce

For each day i, find the day j > i that gives maximum profit.

Code

#include <vector>
#include <iostream>
using namespace std;
int maxProfit(vector<int>& prices) {
    int maxProfit = 0;
    for (int i = 0; i < prices.size(); i++) {        
        for (int j = i + 1; j < prices.size(); j++) {
            if (prices[j] > prices[i]) {
                maxProfit = max(maxProfit, prices[j] - prices[i]);
            }
        }
    }
    return maxProfit;
}
int main() {
    vector<int> prices{7,1,5,3,6,4};
    cout << maxProfit(prices) << endl;
    prices = {7,6,4,3,1};
    cout << maxProfit(prices) << endl;
}

Output:
5
0

Complexity

• Runtime: O(N^2), where N = prices.length.

• Extra space: O(1).

Solution 2: Smallest and largest prices

Given a past day i, the future day j > i that gives the maximum profit is the day that has the largest price which is bigger than prices[i].

Conversely, given a future day j, the past day i < j that gives the maximum profit is the day with the smallest price.

Code

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int maxProfit(vector<int>& prices) {
    int maxProfit = 0;
    int i = 0;
    while (i < prices.size()) {
        while (i < prices.size() - 1 && prices[i] >= prices[i + 1]) {
            i++;
        }
        auto imax = max_element(prices.begin() + i, prices.end());
        auto imin = min_element(prices.begin() + i, imax);
        maxProfit = max(maxProfit, *imax - *imin);
        i = distance(prices.begin(), imax) + 1;
    }
    return maxProfit;
}
int main() {
    vector<int> prices{7,1,5,3,6,4};
    cout << maxProfit(prices) << endl;
    prices = {7,6,4,3,1};
    cout << maxProfit(prices) << endl;
    prices = {2,4,1,7};
    cout << maxProfit(prices) << endl;
    prices = {2,4,1};
    cout << maxProfit(prices) << endl;
}

Output:
5
0
6
2

Complexity

• Runtime: O(N), where N = prices.length.

• Extra space: O(1).

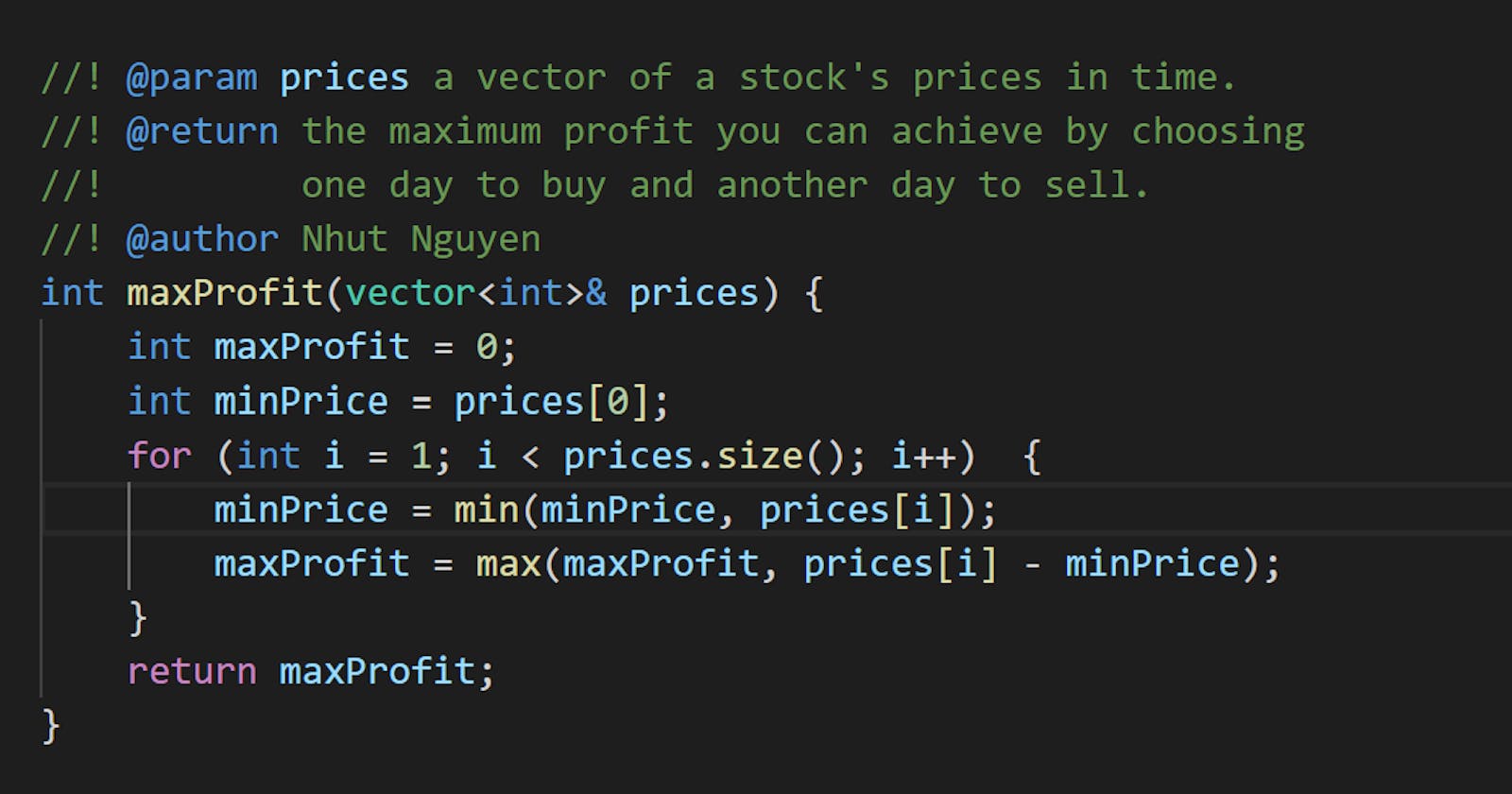
Solution 3: Only the smallest price

Given a future day j, the past day i that gives the maximum profit is the day with minimum price.

Code

#include <vector>
#include <iostream>
using namespace std;
int maxProfit(vector<int>& prices) {
    int maxProfit = 0;
    int minPrice = prices[0];
    for (int i = 1; i < prices.size(); i++)  {
        minPrice = min(minPrice, prices[i]);
        maxProfit = max(maxProfit, prices[i] - minPrice);
    }
    return maxProfit;
}
int main() {
    vector<int> prices{7,1,5,3,6,4};
    cout << maxProfit(prices) << endl;
    prices = {7,6,4,3,1};
    cout << maxProfit(prices) << endl;
    prices = {2,4,1,7};
    cout << maxProfit(prices) << endl;
    prices = {2,4,1};
    cout << maxProfit(prices) << endl;
}

Output:
5
0
6
2

Complexity

• Runtime: O(N), where N = prices.length.

• Extra space: O(1).

References

• https://leetcode.com/problems/best-time-to-buy-and-sell-stock/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.