How to solve Leetcode 797. All Paths From Source to Target
An example of a Depth-first search algorithm
Problem statement
Given a directed acyclic graph (DAG) of n nodes labeled from 0 to n - 1, find all possible paths from node 0 to node n - 1 and return them in any order.
The graph is given as follows: graph[i] is a list of all nodes you can visit from node i (i.e., there is a directed edge from node i to node graph[i][j]).
Example 1
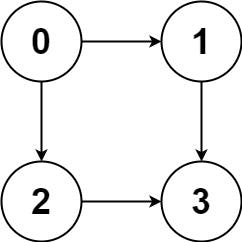
Input: graph = [[1,2],[3],[3],[]]
Output: [[0,1,3],[0,2,3]]
Explanation: There are two paths: `0 -> 1 -> 3` and `0 -> 2 -> 3`.
Example 2
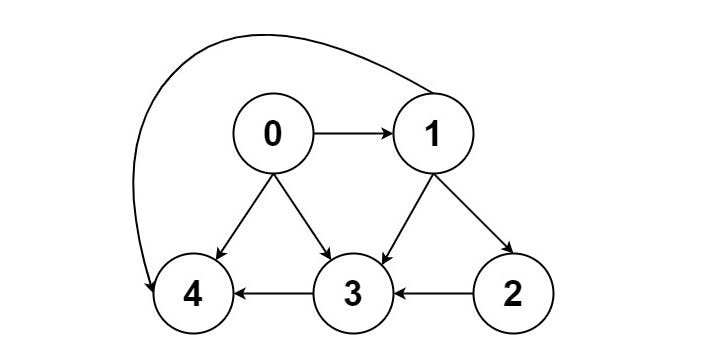
Input: graph = [[4,3,1],[3,2,4],[3],[4],[]]
Output: [[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]
Example 3
Input: graph = [[1],[]]
Output: [[0,1]]
Example 4
Input: graph = [[1,2,3],[2],[3],[]]
Output: [[0,1,2,3],[0,2,3],[0,3]]
Example 5
Input: graph = [[1,3],[2],[3],[]]
Output: [[0,1,2,3],[0,3]]
Constraints
n == graph.length.2 <= n <= 15.0 <= graph[i][j] < n.graph[i][j] != i(i.e., there will be no self-loops).All the elements of
graph[i]are unique.The input graph is guaranteed to be a DAG.
Solution: Depth-first search (DFS)
This problem is exactly the Depth-first search algorithm.
Code
#include <vector>
#include <iostream>
using namespace std;
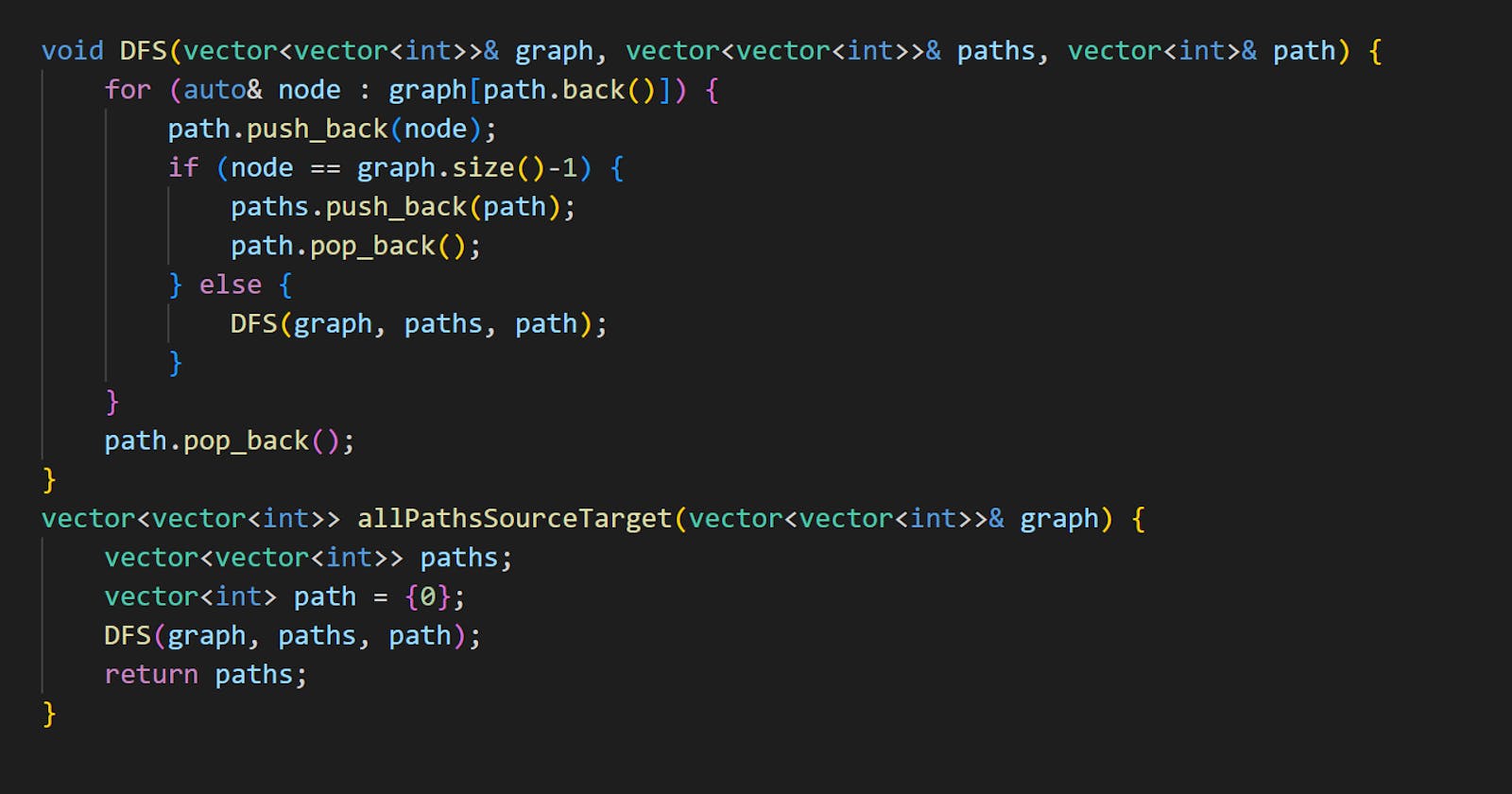
void DFS(vector<vector<int>>& graph, vector<vector<int>>& paths, vector<int>& path) {
for (auto& node : graph[path.back()]) {
path.push_back(node);
if (node == graph.size() - 1) {
paths.push_back(path);
path.pop_back();
} else {
DFS(graph, paths, path);
}
}
path.pop_back();
}
vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
vector<vector<int>> paths;
vector<int> path = {0};
DFS(graph, paths, path);
return paths;
}
void printPaths(vector<vector<int>>& paths) {
cout << "[";
for (auto& p : paths) {
cout << "[";
for (auto& node : p) {
cout << node << ",";
}
cout << "],";
}
cout << "]\n";
}
int main() {
vector<vector<int>> graph = {{1,2},{3},{3},{}};
auto paths = allPathsSourceTarget(graph);
printPaths(paths);
graph = {{4,3,1},{3,2,4},{3},{4},{}};
paths = allPathsSourceTarget(graph);
printPaths(paths);
}
Output:
[[0,1,3,],[0,2,3,],]
[[0,4,],[0,3,4,],[0,1,3,4,],[0,1,2,3,4,],[0,1,4,],]
Complexity
Runtime:
O(N^2), whereN = graph.length.Extra space:
O(N).