How To Solve Leetcode 62. Unique Paths
An example of recursive algorithms and dynamic programming
Problem statement
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
Example 1
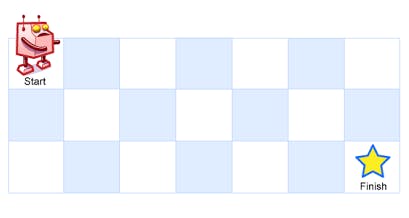
Input: m = 3, n = 7
Output: 28
Example 2
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down
Example 3
Input: m = 7, n = 3
Output: 28
Example 4
Input: m = 3, n = 3
Output: 6
Constraints
1 <= m, n <= 100.It's guaranteed that the answer will be less than or equal to
2*10^9.
Solution 1: Recursive
At each point, the robot has two ways of moving: right or down. Let P(m,n) is the wanted result. Then you have a recursive relationship:
P(m,n) = P(m-1, n) + P(m, n-1)
If the grid has only one row or only one column, then there is only one possible path.
P(1, n) = P(m, 1) = 1.
We have a recursive implementation.
Code
#include <iostream>
#include <vector>
using namespace std;
int uniquePaths(int m, int n) {
if (m == 1 || n == 1) {
return 1;
}
return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
}
int main() {
std::cout << uniquePaths(3,7) << std::endl;
std::cout << uniquePaths(7,3) << std::endl;
std::cout << uniquePaths(3,2) << std::endl;
std::cout << uniquePaths(3,3) << std::endl;
}
Output:
28
28
3
6
Complexity
Runtime:
O(2^m + 2^n), wherem*nis the size of the grid.Extra space:
O(2^m + 2^n).
Solution 2: Dynamic programming
The recursive implementation repeats a lot of computations.
For example, uniquePaths(2,2) was recomputed in both uniquePaths(2,3) and uniquePaths(3,2) when you compute uniquePaths(3,3).
One way of storing what has been computed is by using dynamic programming.
Code
#include <iostream>
#include <vector>
using namespace std;
int uniquePaths(int m, int n) {
vector<vector<int> > dp(m, vector<int>(n,1));
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
int main() {
std::cout << uniquePaths(3,7) << std::endl;
std::cout << uniquePaths(7,3) << std::endl;
std::cout << uniquePaths(3,2) << std::endl;
std::cout << uniquePaths(3,3) << std::endl;
}
Output:
28
28
3
6
Complexity
Runtime:
O(m*n), wherem*nis the size of the grid.Extra space:
O(m*n).
Solution 3: Reduced dynamic programming
You can rephrase the relationship inside the loop like this:
"new value" = "old value" + "previous value";
Then you do not have to store all values of all rows.
Code
#include <iostream>
#include <vector>
using namespace std;
int uniquePaths(int m, int n) {
vector<int> dp(n, 1);
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[j] += dp[j - 1];
}
}
return dp[n - 1];
}
int main() {
std::cout << uniquePaths(3,7) << std::endl;
std::cout << uniquePaths(7,3) << std::endl;
std::cout << uniquePaths(3,2) << std::endl;
std::cout << uniquePaths(3,3) << std::endl;
}
Output:
28
28
3
6
Complexity
Runtime
O(m*n).Memory
O(n).
Final thought
I am wondering if there is some mathematics behind this problem. Please share your finding if you find a formula for the solution to this problem.

