Problem statement

Design a class to find the k-th largest element in a stream. Note that it is the k-th largest element in the sorted order, not the k-th distinct element.

Implement KthLargest class:

• KthLargest(int k, int[] nums) Initializes the object with the integer k and the stream of integers nums.

• int add(int val) Appends the integer val to the stream and returns the element representing the k-th largest element in the stream.

Example 1

Input
["KthLargest", "add", "add", "add", "add", "add"]
[[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
Output
[null, 4, 5, 5, 8, 8]

Explanation
KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
kthLargest.add(3);   // return 4
kthLargest.add(5);   // return 5
kthLargest.add(10);  // return 5
kthLargest.add(9);   // return 8
kthLargest.add(4);   // return 8

Constraints

• 1 <= k <= 10^4.

• 0 <= nums.length <= 10^4.

• -10^4 <= nums[i] <= 10^4.

• -10^4 <= val <= 10^4.

• At most 10^4 calls will be made to add.

• It is guaranteed that there will be at least k elements in the array when you search for the k-th element.

Solution 1: Sort and Append

Sort the stream when initialization. And keep it sorted whenever you append a new value.

Example 1

For nums = [4, 5, 8, 2] and k = 3.

• Sort nums = [8, 5, 4, 2].

• Adding 3 to nums. It becomes [8, 5, 4, 3, 2]. The third largest element is 4.

• Adding 5 to nums. It becomes [8, 5, 5, 4, 3, 2]. The third largest element is 5.

• Adding 10 to nums. It becomes [10, 8, 5, 5, 4, 3, 2]. The third largest element is 5.

• So on and so on.

Code

#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
class KthLargest {
    vector<int> _nums;
    int _k;
public:
    KthLargest(int k, vector<int>& nums) : _nums(nums), _k(k) {   
        sort(_nums.begin(), _nums.end(), std::greater());
    }

    int add(int val) {
        auto it = _nums.begin();
        while (it != _nums.end() &&  val < *it) {
            it++;
        }
        _nums.insert(it, val);
        return *(_nums.begin() + _k - 1);
    }
};
int main() {
    vector<int> nums{4,5,8,2};
    KthLargest a(3, nums);
    cout << a.add(3) << endl;
    cout << a.add(5) << endl;
    cout << a.add(10) << endl;
    cout << a.add(9) << endl;
    cout << a.add(4) << endl;
}

Output:
4
5
5
8
8

Complexity

• Runtime: O(NlogN), where N = nums.length.

• Extra space: O(1).

Solution 2: Priority queue

There is a data structure that has the property you want in this problem.

It is std::priority_queue, which keeps its top element is always the largest one according to the comparison you define for the queue.

By default, the "less than" comparison is used for std::priority_queue and the top one is always the biggest element.

If you want the top one is always the smallest element, you can use the comparison "greater than" for your queue.

Code

#include <vector>
#include <queue>
#include <iostream>
using namespace std;
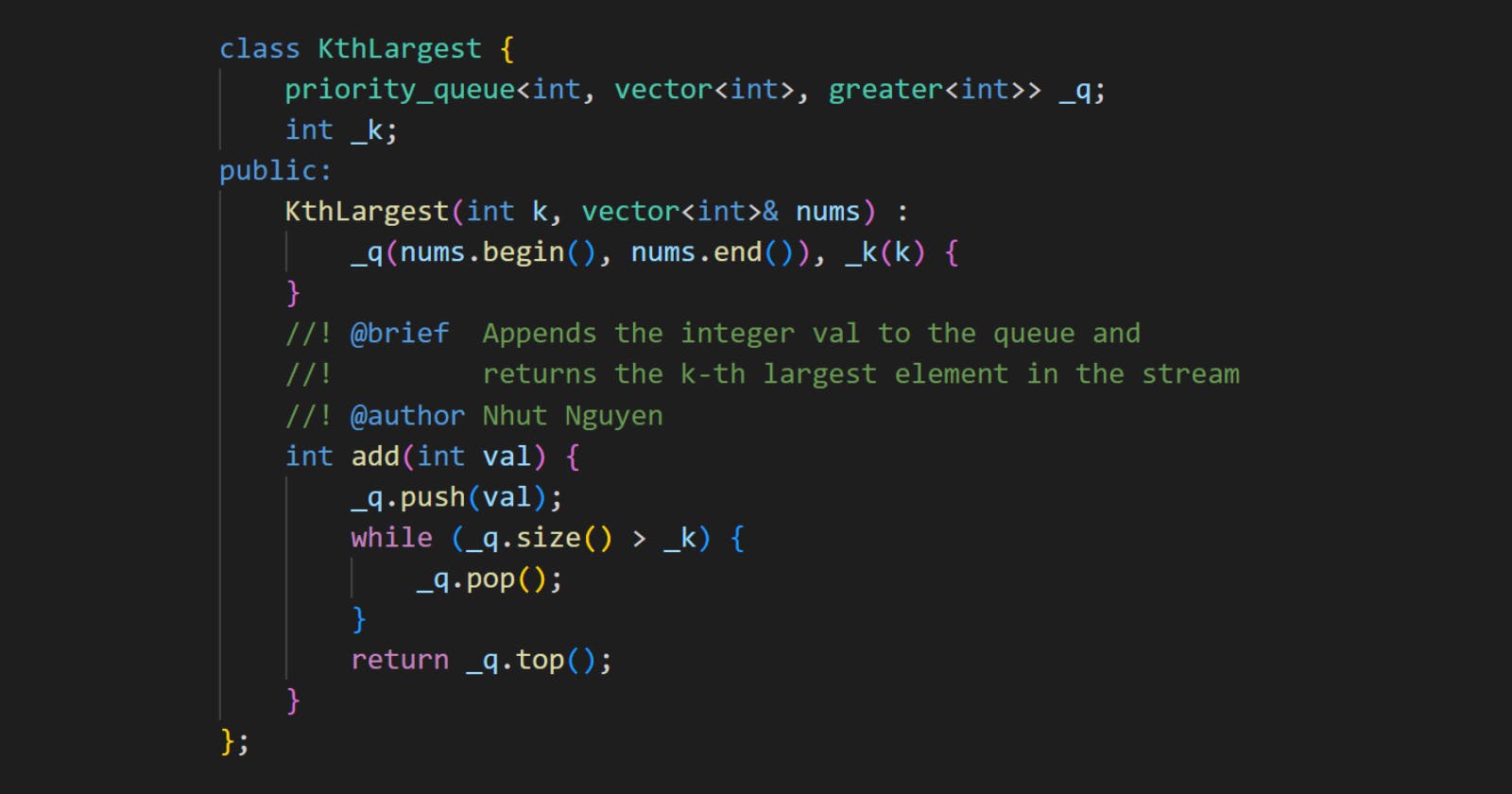
class KthLargest {
    priority_queue<int, vector<int>, greater<int>> _q;
    int _k;
public:
    KthLargest(int k, vector<int>& nums) : 
        _q(nums.begin(), nums.end()), _k(k) {
    }

    int add(int val) {
        _q.push(val);
        while (_q.size() > _k) {
            _q.pop();
        }
        return _q.top();
    }
};
int main() {
    vector<int> nums{4,5,8,2};
    KthLargest a(3, nums);
    cout << a.add(3) << endl;
    cout << a.add(5) << endl;
    cout << a.add(10) << endl;
    cout << a.add(9) << endl;
    cout << a.add(4) << endl;
}

Output:
4
5
5
8
8

Complexity

• Runtime: O(N), where N = nums.length.

• Extra space: O(1).

References

• https://leetcode.com/problems/kth-largest-element-in-a-stream/

• https://en.cppreference.com/w/cpp/container/priority_queue

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.