Problem statement

Given an integer array nums, you need to find one continuous subarray that if you only sort this subarray in ascending order, then the whole array will be sorted in ascending order.

Return the shortest such subarray and output its length.

Example 1

Input: nums = [2,6,4,8,10,9,15]
Output: 5
Explanation: You need to sort [6, 4, 8, 10, 9] in ascending order to make the whole array sorted in ascending order.

Example 2

Input: nums = [1,2,3,4]
Output: 0

Example 3

Input: nums = [1]
Output: 0

Constraints:

• 1 <= nums.length <= 10^4.

• -10^5 <= nums[i] <= 10^5.

Follow up: Can you solve it in O(n) time complexity?

Solution 1: Sort and compare the difference

Example 1

Comparing nums = [2,6,4,8,10,9,15] with its sorted one sortedNums = [2,4,6,8,9,10,15]:

• The first position that makes the difference is left = 1, where 6 != 4.

• The last position that makes the difference is right = 5, where 9 != 10.

• The length of that shortest subarray is right - left + 1 = 5.

Code

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int findUnsortedSubarray(vector<int>& nums) {
    vector<int> sortedNums = nums;
    sort(sortedNums.begin(), sortedNums.end());
    int left = 0;
    while (left < nums.size() && nums[left] == sortedNums[left]) {
        left++;
    }
    int right = nums.size() - 1;
    while (right >= 0 && nums[right] == sortedNums[right]) {
        right--;
    }
    return left >= right ? 0 : right - left + 1;
}
int main() {
    vector<int> nums{2,6,4,8,10,9,15};
    cout << findUnsortedSubarray(nums) << endl;
    nums = {1,2,3,4};
    cout << findUnsortedSubarray(nums) << endl;
    nums = {1};
    cout << findUnsortedSubarray(nums) << endl;
}

Output:
5
0
0

Complexity

• Runtime: O(nlogn), where n = nums.length because of the sorting algorithm.

• Extra space: O(n).

Solution 2: Comparing only maximum and minimum elements

Assume the subarray A = [nums[0], ..., nums[i - 1]] is sorted. What would be the wanted right position for the subarray B = [nums[0], ..., nums[i - 1], nums[i]]?

If nums[i] is smaller than max(A), the longer subarray B is not in ascending order. You might need to sort it, which means right = i.

Similarly, assume the subarray C = [nums[j + 1], ..., nums[n - 1]] is sorted. What would be the wanted left position for the subarray D = [nums[j], nums[j + 1], ..., nums[n - 1]]?

If nums[j] is bigger than min(C), the longer subarray D is not in ascending order. You might need to sort it, which means left = j

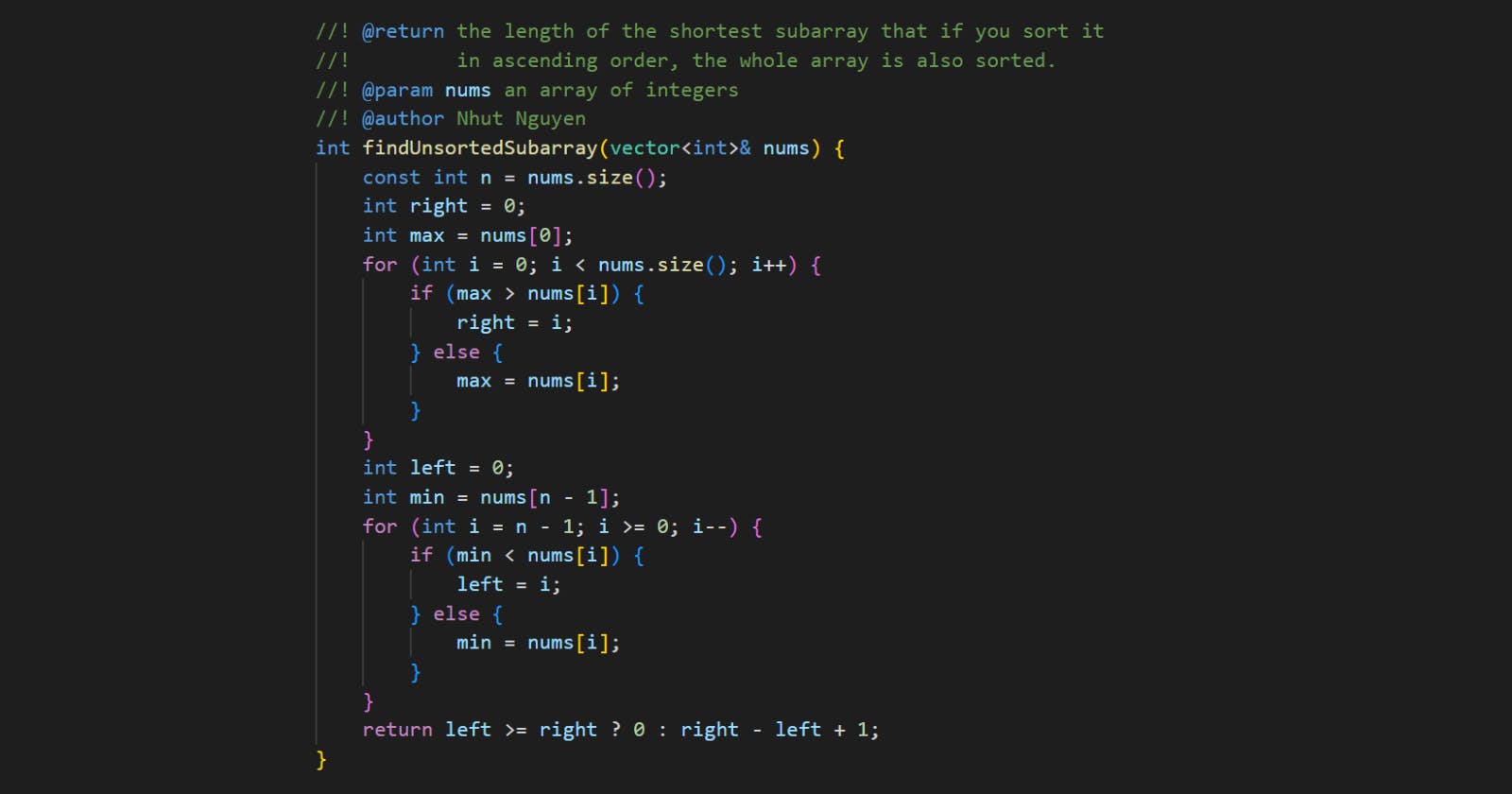
Code

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int findUnsortedSubarray(vector<int>& nums) {
    const int n = nums.size();
    int left = n - 1;
    int min = nums[n - 1];
    for (int i = n - 1; i >= 0; i--) {
        if (min < nums[i]) {
            left = i;
        } else {
            min = nums[i];
        }
    }
    int right = 0;
    int max = nums[0];
    for (int i = 0; i < nums.size(); i++) {
        if (max > nums[i]) {
            right = i;
        } else {
            max = nums[i];
        }
    }
    return left >= right ? 0 : right - left + 1;
}
int main() {
    vector<int> nums{2,6,4,8,10,9,15};
    cout << findUnsortedSubarray(nums) << endl;
    nums = {1,2,3,4};
    cout << findUnsortedSubarray(nums) << endl;
    nums = {1};
    cout << findUnsortedSubarray(nums) << endl;
}

Output:
5
0
0

Complexity

• Runtime: O(n), where n = nums.length.

• Extra space: O(1).

Conclusion

Solution 2 helped you identify the shortest subarray (by the left and right indices) needed to be sorted in order to sort the whole array.

That means in some cases you can sort an array with complexity O(N + mlogm) < O(NlogN) where N is the length of the whole array and m is the length of the shortest subarray.

References

• https://leetcode.com/problems/shortest-unsorted-continuous-subarray/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book "10 Classic Coding Challenges".