Problem statement

You are given an integer array nums of length n where nums is a permutation of the numbers in the range [0, n - 1].

You should build a set s[k] = {nums[k], nums[nums[k]], nums[nums[nums[k]]], ... } subjected to the following rule:

• The first element in s[k] starts with the element nums[k].

• The next element in s[k] should be nums[nums[k]], and then nums[nums[nums[k]]], and so on.

• We stop adding elements before a duplicate element occurs in s[k].

Return the length of the longest set s[k].

Example 1

Input: nums = [5,4,0,3,1,6,2]
Output: 4
Explanation: 
nums[0] = 5, nums[1] = 4, nums[2] = 0, nums[3] = 3, nums[4] = 1, nums[5] = 6, nums[6] = 2.
One of the longest sets s[k]:
s[0] = {nums[0], nums[5], nums[6], nums[2]} = {5, 6, 2, 0}

Example 2

Input: nums = [0,1,2]
Output: 1

Constraints:

• 1 <= nums.length <= 10^5.

• 0 <= nums[i] < nums.length.

• All the values of nums are unique.

Solution: Understanding the math behind

A permutation is a one-to-one mapping from a set of integers to itself.

The permutation on the set nums in this problem is defined by the mapping i -> nums[i]. For instance in Example 1, the permutation is defined as following:

0 -> 5,
1 -> 4,
2 -> 0,
3 -> 3,
4 -> 1,
5 -> 6,
6 -> 2.

You can always rearrange the definition of a permutation into groups of cyclic chains (factors).

0 -> 5, 5 -> 6, 6 -> 2, 2 -> 0,
1 -> 4, 4 -> 1,
3 -> 3

The set s[k] in this problem is such a chain. In mathematics, it is called a cycle; because the chain (0, 5, 6, 2) is considered the same as (5, 6, 2, 0), (6, 2, 0, 5) or (2, 0, 5, 6) in Example 1.

Assume you have used some elements of the array nums to construct some cycles. To construct another one, you should start with the unused elements.

The problem leads to finding the longest cycle of a given permutation.

Code

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
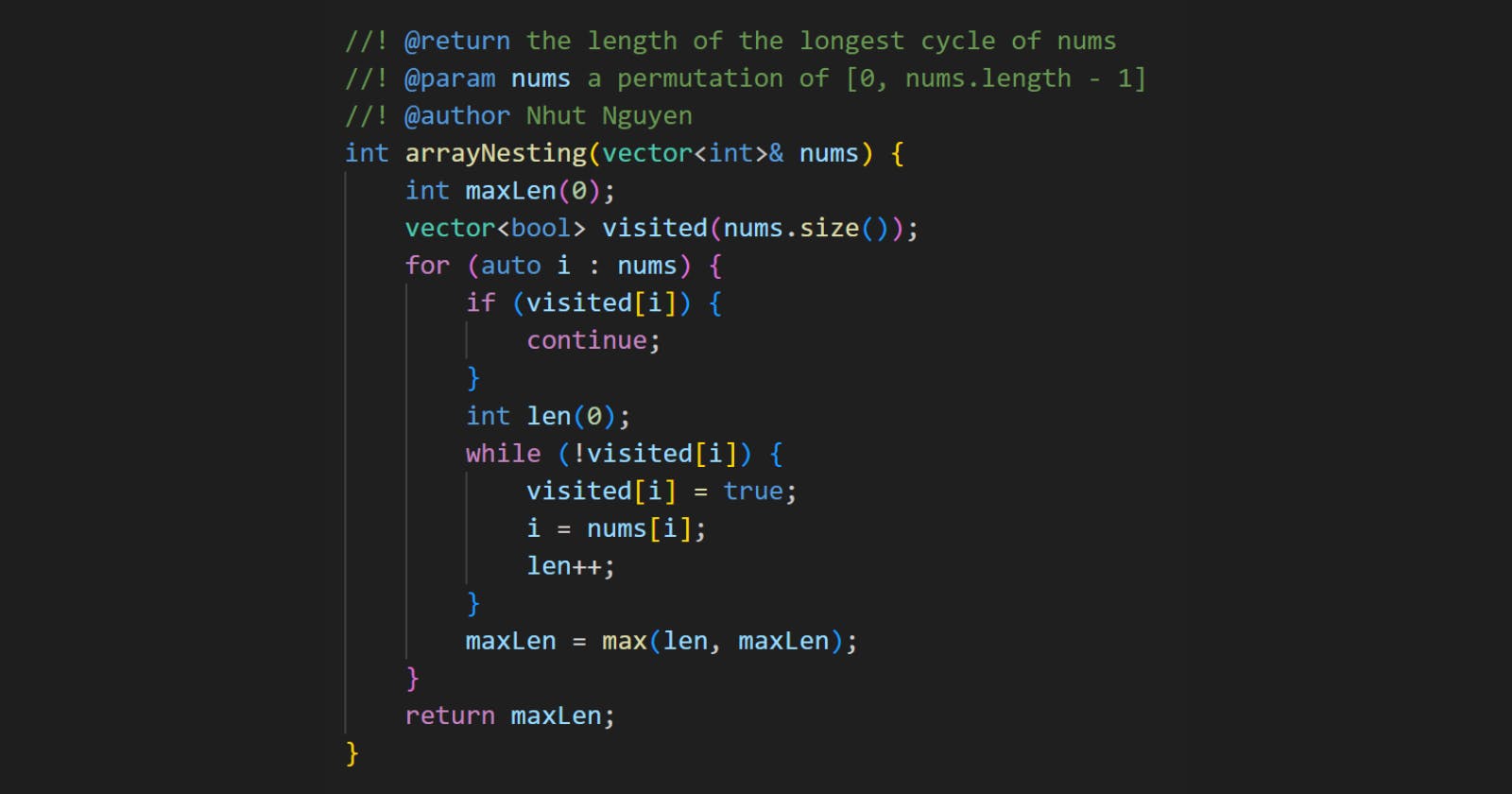
int arrayNesting(vector<int>& nums) {
    int maxLen(0);
    vector<bool> visited(nums.size());
    for (auto i : nums) {
        if (visited[i]) {
            continue;
        }
        int len(0);
        while (!visited[i]) {
            visited[i] = true;
            i = nums[i];            
            len++;
        }
        maxLen = max(len, maxLen);
    }
    return maxLen;
}

int main() {
    vector<int> nums = {5,4,0,3,1,6,2}; 
    cout << arrayNesting(nums) << endl;
    nums = {0,1,2}; 
    cout << arrayNesting(nums) << endl;
    nums = {0,2,1}; 
    cout << arrayNesting(nums) << endl;
    nums = {2,0,1}; 
    cout << arrayNesting(nums) << endl;
}

Output:
4
1
2
3

Complexity

• Runtime: O(N), where N = nums.length.

• Extra space: much less than O(N) since vector<bool> is optimized for space efficiency.

---

Thanks for reading. Feel free to share your thought about my content and check out my FREE book 10 Classic Coding Challenges.

What is your approach? The problem was picked from leetcode.com. You can submit your solution in any programming language and check the performance.