Problem statement

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.

A subarray is a contiguous part of an array.

Example 1

Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.

Example 2

Input: nums = [1]
Output: 1

Example 3

Input: nums = [5,4,-1,7,8]
Output: 23

Constraints

• 1 <= nums.length <= 10^5.

• -10^4<= nums[i] <= 10^4.

Solution

The subarrays you want to find should not have negative prefix sums. A negative prefix sum would make the sum of the subarray smaller.

Example 1

For nums = [-2,1,-3,4,-1,2,1,-5,4], [-2] or [-2,1] or [-2,1,-3] should not be a prefix of the subarrays you want to find. Since it makes the sum of the result smaller.

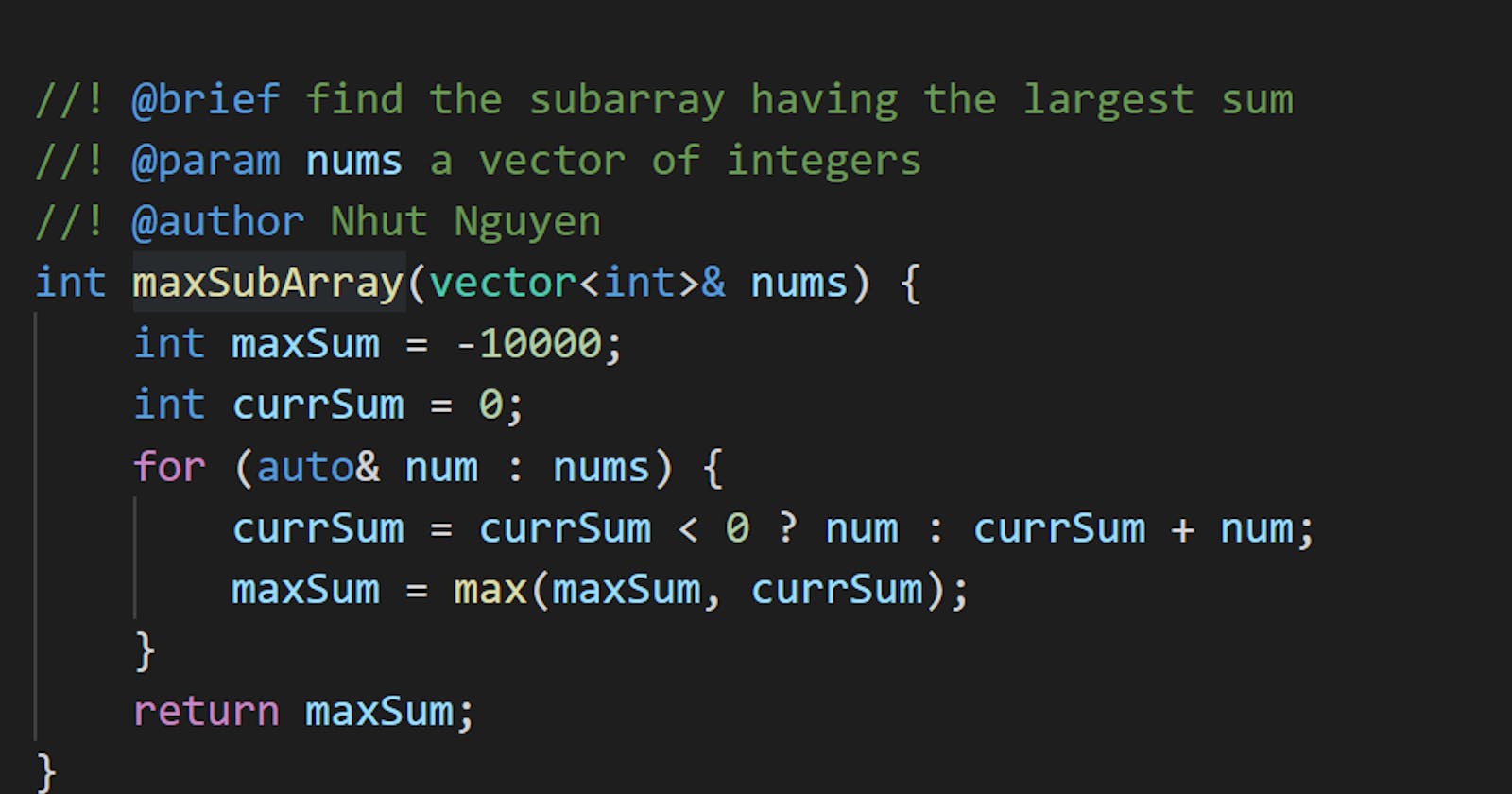
Code

int maxSubArray(vector<int>& nums) {
    int maxSum = -10000;
    int currSum = 0;
    for (auto& num : nums) {
        currSum = currSum < 0 ? num : currSum + num;
        maxSum = max(maxSum, currSum);
    }
    return maxSum;
}
int main() {
    vector<int> nums = {-2,1,-3,4,-1,2,1,-5,4};
    cout << maxSubArray(nums) << endl;
    nums = {1};
    cout << maxSubArray(nums) << endl;
    nums = {5,4,-1,7,8};
    cout << maxSubArray(nums) << endl;
}

Output:
6
1
23

Complexity

• Runtime: O(N), where N = nums.length.

• Extra space: O(1).

References

• https://leetcode.com/problems/maximum-subarray/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.