Problem statement

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.

Given n, calculate F(n).

Example 1

Input: n = 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2

Input: n = 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3

Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

Constraints

• 0 <= n <= 30.

Solution 1: Recursive

#include <iostream>
int fib(int n) {
    if (n <= 1) {
        return n;
    } 
    return fib(n - 1) + fib(n - 2);
}
int main() {
    std::cout << fib(2) << std::endl;
    std::cout << fib(3) << std::endl;
    std::cout << fib(4) << std::endl;
}

Output:
1
2
3

Complexity

• Runtime: O(2^n).

• Extra space: O(2^n).

Solution 2: Dynamic programming

#include <iostream>
#include <vector>
int fib(int n) {
    if (n <= 1) {
        return n;
    }
    std::vector<int> f(n + 1);
    f[0] = 0;
    f[1] = 1;
    for (int i = 2; i <= n; i++) {
        f[i] = f[i - 1] + f[i - 2];
    }
    return f[n];
}
int main() {
    std::cout << fib(2) << std::endl;
    std::cout << fib(3) << std::endl;
    std::cout << fib(4) << std::endl;
}

Output:
1
2
3

Complexity

• Runtime: O(n).

• Extra space: O(n).

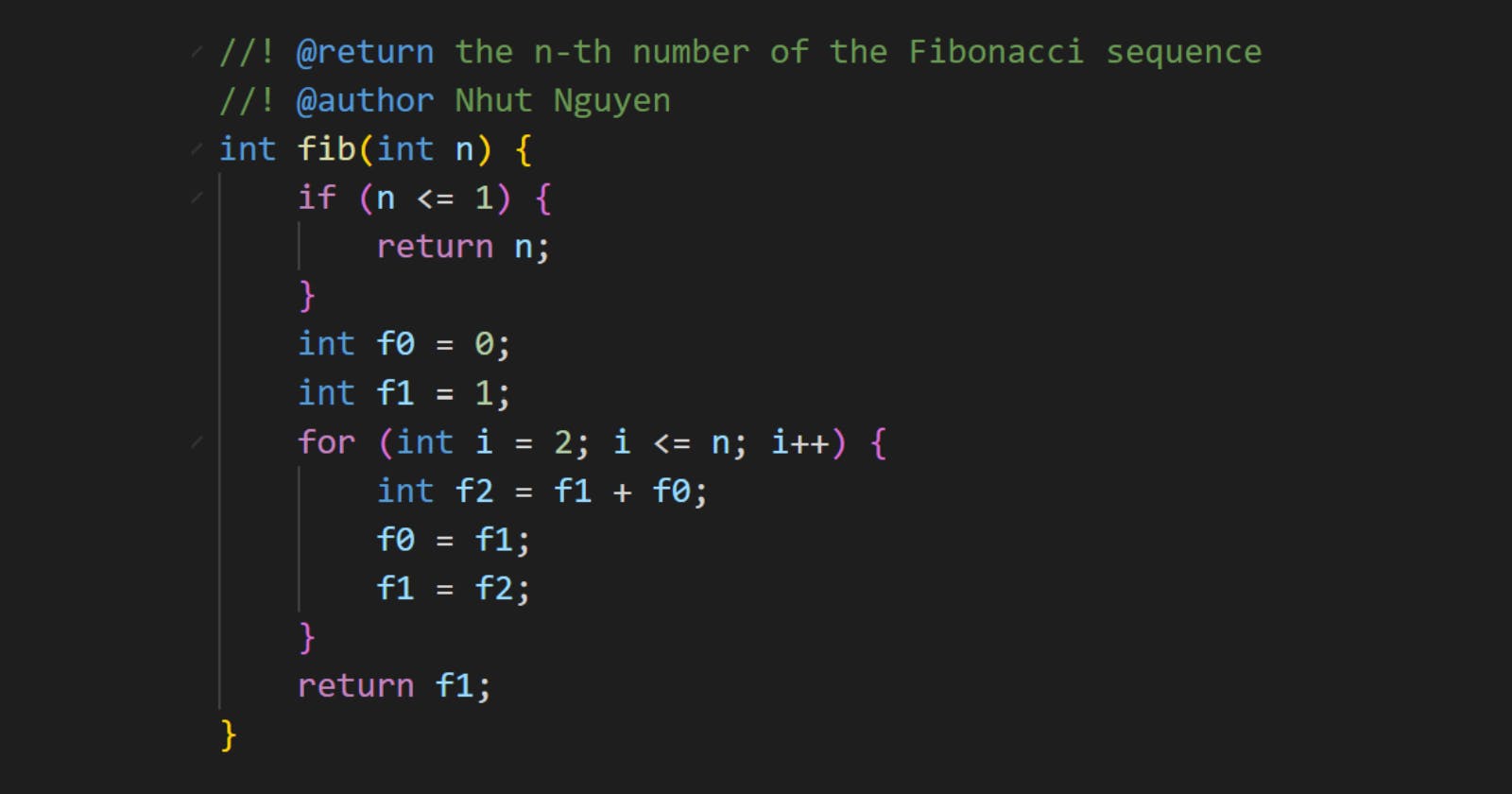
Solution 3: Reduce space for dynamic programming

#include <iostream>
#include <vector>
int fib(int n) {
    if (n <= 1) {
        return n;
    }
    int f0 = 0;
    int f1 = 1;
    for (int i = 2; i <= n; i++) {
        int f2 = f1 + f0;
        f0 = f1;
        f1 = f2;
    }
    return f1;
}
int main() {
    std::cout << fib(2) << std::endl;
    std::cout << fib(3) << std::endl;
    std::cout << fib(4) << std::endl;
}

Output:
1
2
3

Complexity

• Runtime: O(n).

• Extra space: O(1).

---

You can try to solve this problem by yourself at leetcode.com/problems/fibonacci-number

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.