Problem statement

The Hamming distance between two integers is the number of positions at which the corresponding bits are different.

Given two integers x and y, return the Hamming distance between them.

Example 1

Input: x = 1, y = 4
Output: 2
Explanation:
1   (0 0 0 1)
4   (0 1 0 0)
       ↑   ↑
The above arrows point to positions where the corresponding bits are different.

Example 2

Input: x = 3, y = 1
Output: 1

Constraints

• 0 <= x, y <= 2^31.

Solution: Using bitwise operator XOR

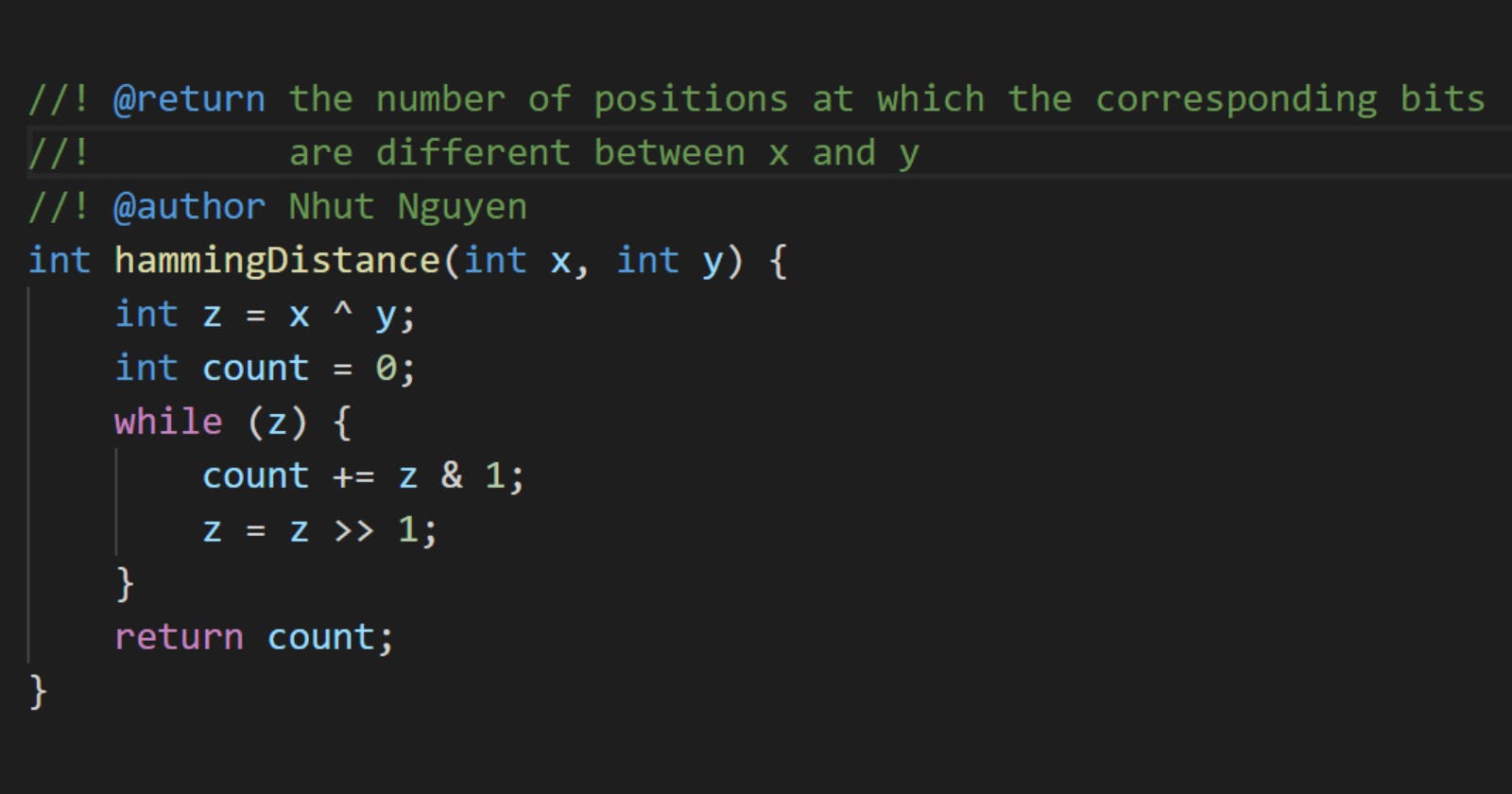
You could use bit operator ^ (XOR) to get the bit positions where x and y are different. Then use bit operator & (AND) at each position to count them.

Code

#include <iostream>
int hammingDistance(int x, int y) {
    int z = x ^ y;
    int count = 0;
    while (z) {
        count += z & 1;
        z = z >> 1;
    }
    return count;
}
int main() {
    std::cout << hammingDistance(1,4) << std::endl;
    std::cout << hammingDistance(1,3) << std::endl;
}

Output:
2
1

Complexity

• Runtime: O(1).

• Extra space: O(1).

References

• https://leetcode.com/problems/hamming-distance/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.