Problem statement

A wiggle sequence is a sequence where the differences between successive numbers strictly alternate between positive and negative. The first difference (if one exists) may be either positive or negative. A sequence with one element and a sequence with two non-equal elements are trivially wiggle sequences.

• For example, [1, 7, 4, 9, 2, 5] is a wiggle sequence because the differences (6, -3, 5, -7, 3) alternate between positive and negative.

• In contrast, [1, 4, 7, 2, 5] and [1, 7, 4, 5, 5] are not wiggle sequences. The first is not because its first two differences are positive, and the second is not because its last difference is zero.

A subsequence is obtained by deleting some elements (possibly zero) from the original sequence, leaving the remaining elements in their original order.

Given an integer array nums, return the length of the longest wiggle subsequence of nums.

Example 1

Input: nums = [1,7,4,9,2,5]
Output: 6
Explanation: The entire sequence is a wiggle sequence with differences (6, -3, 5, -7, 3).

Example 2

Input: nums = [1,17,5,10,13,15,10,5,16,8]
Output: 7
Explanation: There are several subsequences that achieve this length.
One is [1, 17, 10, 13, 10, 16, 8] with differences (16, -7, 3, -3, 6, -8).

Example 3

Input: nums = [1,2,3,4,5,6,7,8,9]
Output: 2

Constraints

• 1 <= nums.length <= 1000.

• 0 <= nums[i] <= 1000.

Follow up: Could you solve this in O(n) time?

Solution: Counting the local extrema of nums

First, if you pick all local extrema (minima and maxima) of nums to form a subsequence e, then it is wiggle. Let us call it an extrema subsequence.

Example 2

For nums = [1,17,5,10,13,15,10,5,16,8], the local extrema are [1,17,5,15,5,16,8]. It is wiggle and called extrema subsequence.

Note that if nums.length = n then nums[0] and nums[n - 1] are always the first and the last extremum.

Second, given any two successive local extrema a and b, you cannot have any wiggle subsequence between them. Because the elements between them are either monotonic increasing or decreasing.

That proves the extrema subsequence is the longest wiggle one.

Code

#include <iostream>
#include <vector>
using namespace std;
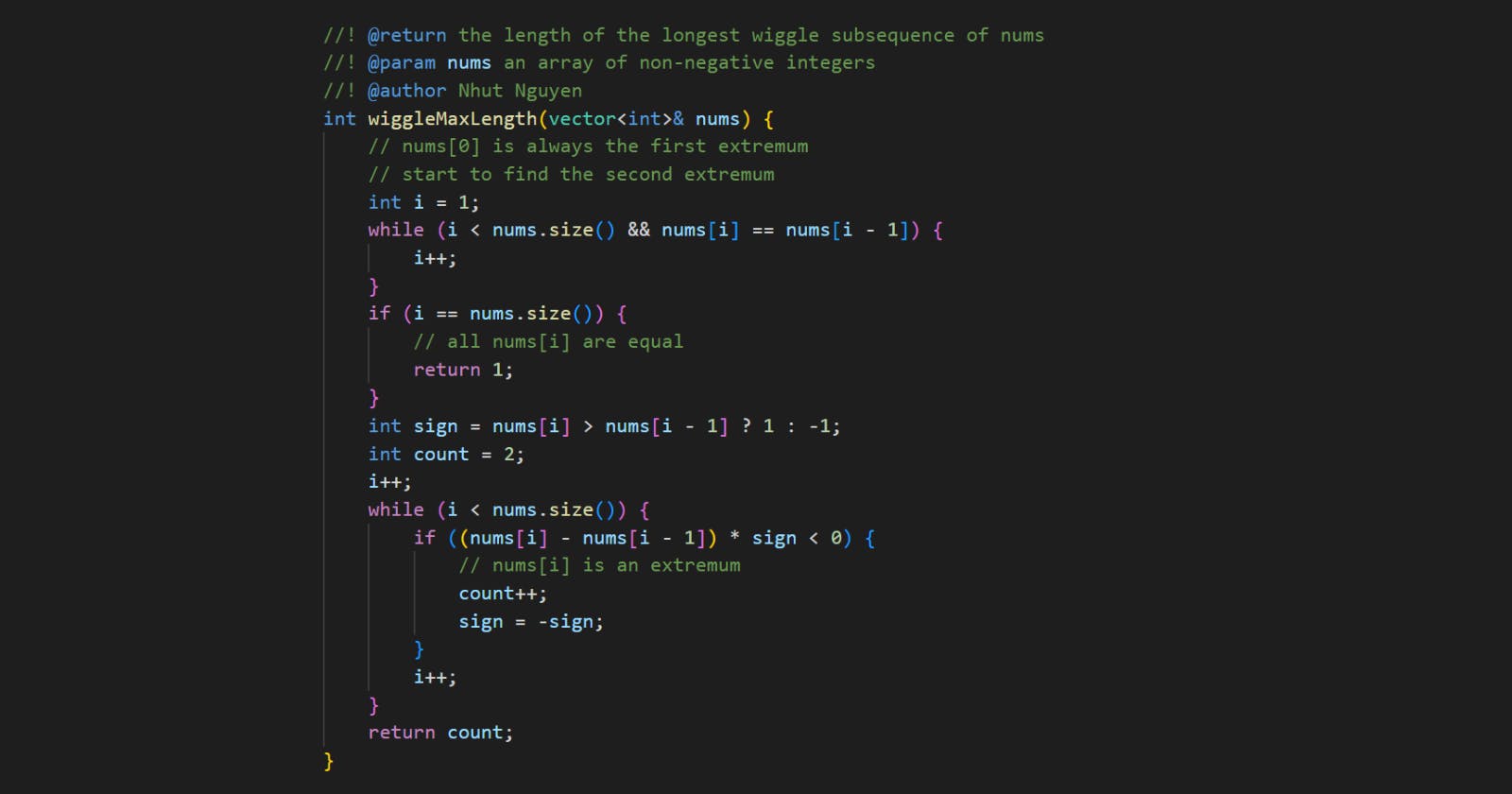
int wiggleMaxLength(vector<int>& nums) {
    // nums[0] is always the first extremum
    // start to find the second extremum
    int i = 1;
    while (i < nums.size() && nums[i] == nums[i - 1]) {
        i++;
    }
    if (i == nums.size()) {
        // all nums[i] are equal
        return 1;
    }
    int sign = nums[i] > nums[i - 1] ? 1 : -1;
    int count = 2;
    i++;
    while (i < nums.size()) {
        if ((nums[i] - nums[i - 1]) * sign < 0) {
            // nums[i] is an extremum
            count++;
            sign = -sign;
        }
        i++;
    }
    return count;
}
int main() {
    vector<int> nums{1,7,4,9,2,5};
    cout << wiggleMaxLength(nums) << endl;
    nums = {1,17,5,10,13,15,10,5,16,8};
    cout << wiggleMaxLength(nums) << endl;
    nums = {1,2,3,4,5,6,7,8,9};
    cout << wiggleMaxLength(nums) << endl;
}

Output:
6
7
2

Complexity

• Runtime: O(n), where n = nums.length.

• Extra space: O(1).

References

• https://leetcode.com/problems/wiggle-subsequence/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.