Problem statement

Given a string array words, return the maximum value of length(word[i]) * length(word[j]) where the two words do not share common letters. If no such two words exist, return 0.

Example 1

Input: words = ["abcw","baz","foo","bar","xtfn","abcdef"]
Output: 16
Explanation: The two words can be "abcw", "xtfn".

Example 2

Input: words = ["a","ab","abc","d","cd","bcd","abcd"]
Output: 4
Explanation: The two words can be "ab", "cd".

Example 3

Input: words = ["a","aa","aaa","aaaa"]
Output: 0
Explanation: No such pair of words.

Constraints

• 2 <= words.length <= 1000.

• 1 <= words[i].length <= 1000.

• words[i] consists only of lowercase English letters.

Solution 1: Bruteforce

For each words[i], for all words[j] with j > i, check if they do not share common letters and compute the product of their lengths.

Code

#include <vector>
#include <iostream>
using namespace std;
int maxProduct(vector<string>& words) {
    int maxP = 0;
    for (int i = 0; i < words.size(); i++) {
        vector<bool> visited(26, false);
        for (char c : words[i]) {
            visited[c - 'a'] = true;
        }        
        for (int j = i + 1; j < words.size(); j++) {
            bool found = false;
            for (char c : words[j]) {              
                if (visited[c - 'a']) {
                    found = true;
                    break;
                }
            }
            if (!found) {
                maxP = max(maxP, (int) (words[i].length() * words[j].length()));
            } 
        }
    }
    return maxP;
}
int main() {
    vector<string> words{"abcw","baz","foo","bar","xtfn","abcdef"};
    cout << maxProduct(words) << endl;
    words = {"a","ab","abc","d","cd","bcd","abcd"};
    cout << maxProduct(words) << endl;
    words = {"a","aa","aaa","aaaa"};
    cout << maxProduct(words) << endl;
}

Output:
16
4
0

Complexity

• Runtime: O(N^2**M), where N = words.length, M = avg(words[i].length).

• Extra space: O(1).

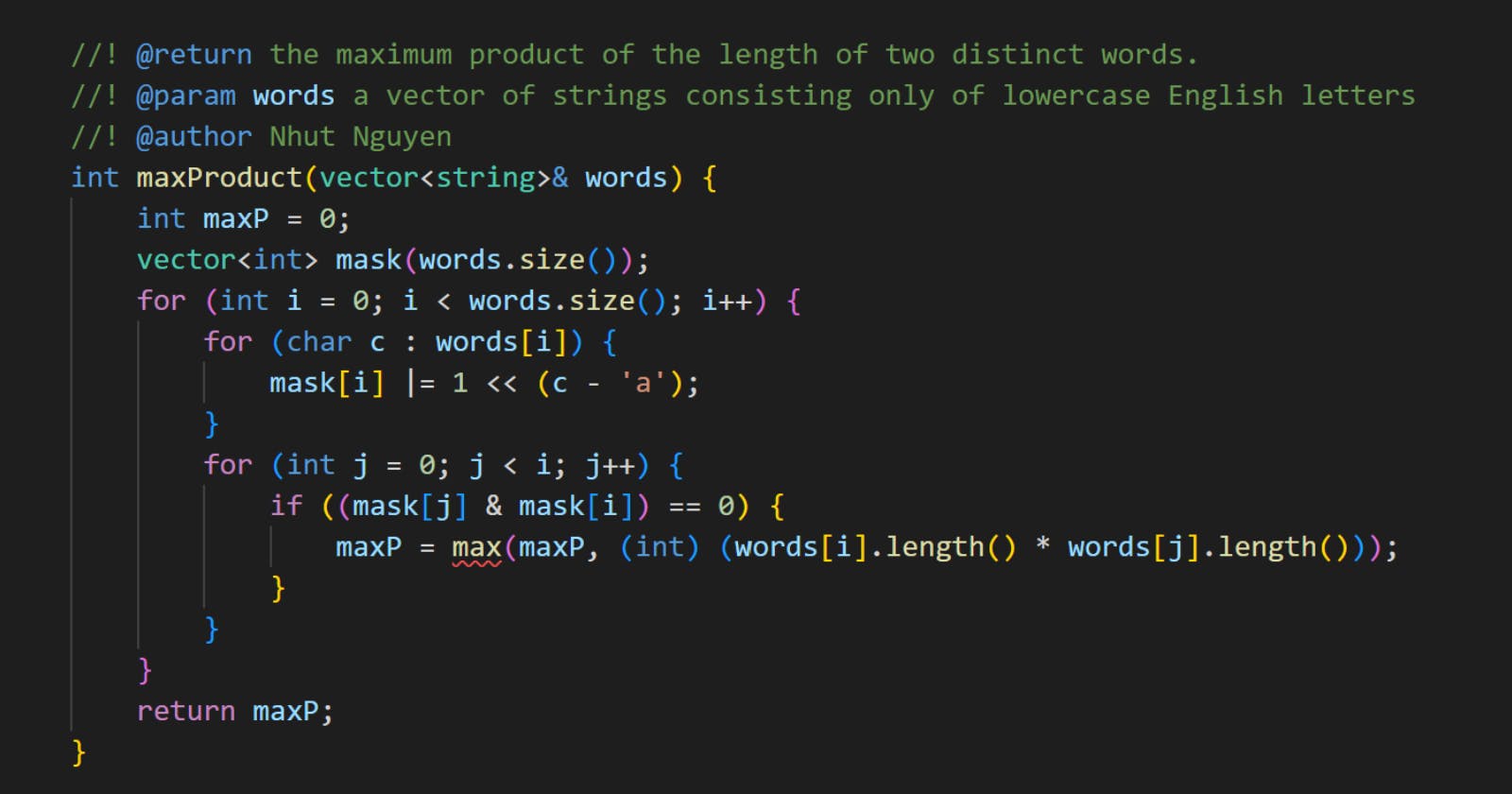
Solution 2: Checking common letters using bit masking

You can map a words[i] to the bit representation of an integer n by their characters like the following:

• If the word words[i] contains the letter 'a', the bit at position 0 of n is 1.

• If the word words[i] contains the letter 'b', the bit at position 1 of n is 1.

• ...

• If the word words[i] contains the letter 'z', the bit at position 25 of n is 1.

Then to check if two words have common letters, you just perform the bitwise operator AND on them.

For Example 1:

• The word "abcw" is mapped to 00010000000000000000000111.

• The word "baz" is mapped to 10000000000000000000000011.

• "abcw" & "baz" = 00000000000000000000000011. This value is not zero, which means they have common letters.

This technique is called bit masking.

Code

#include <vector>
#include <iostream>
using namespace std;
int maxProduct(vector<string>& words) {
    int maxP = 0;
    vector<int> mask(words.size());
    for (int i = 0; i < words.size(); i++) {
        for (char c : words[i]) {
            mask[i] |= 1 << (c - 'a');
        }        
        for (int j = 0; j < i; j++) {
            if ((mask[j] & mask[i]) == 0) {
                maxP = max(maxP, (int) (words[i].length() * words[j].length()));
            } 
        }
    }
    return maxP;
}
int main() {
    vector<string> words{"abcw","baz","foo","bar","xtfn","abcdef"};
    cout << maxProduct(words) << endl;
    words = {"a","ab","abc","d","cd","bcd","abcd"};
    cout << maxProduct(words) << endl;
    words = {"a","aa","aaa","aaaa"};
    cout << maxProduct(words) << endl;
}

Output:
16
4
0

Complexity

• Runtime: O(N^2), where N = words.length.

• Extra space: O(N).

References

• https://leetcode.com/problems/maximum-product-of-word-lengths/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.