Problem statement

Given an array of integers nums containing n + 1 integers where each integer is in the range [1, n] inclusive.

There is only one repeated number in nums, return this repeated number.

You must solve the problem without modifying the array nums and uses only constant extra space.

Example 1

Input: nums = [1,3,4,2,2]
Output: 2

Example 2

Input: nums = [3,1,3,4,2]
Output: 3

Constraints

• 1 <= n <= 10^5.

• nums.length == n + 1.

• 1 <= nums[i] <= n.

• All the integers in nums appear only once except for precisely one integer which appears two or more times.

Follow up:

• How can we prove that at least one duplicate number must exist in nums?

• Can you solve the problem in linear runtime complexity?

Solution 1: Sorting

#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int findDuplicate(vector<int>& nums) {
    sort(nums.begin(), nums.end());
    for (int i = 0; i < nums.size() - 1; i++) {
        if (nums[i] == nums[i + 1]) {
            return nums[i];
        }
    }
    return 0;
}
int main() {
    vector<int> nums{1,3,4,2,2};
    cout << findDuplicate(nums) << endl;
    nums = {3,1,3,4,2};
    cout << findDuplicate(nums) << endl;
}

Output:
2
3

Complexity

• Runtime: O(NlogN), where N = nums.length.

• Extra space: O(1).

Follow up

How can we prove that at least one duplicate number must exist in nums?

Due to Pigeonhole principle:

Here there are n + 1 pigeons in n holes. The pigeonhole principle says that at least one hole has more than one pigeon.

Can you solve the problem in linear runtime complexity?

Here are a few solutions.

Solution 2: Marking the visited numbers

Code

#include <vector>
#include <iostream>
using namespace std;
int findDuplicate(vector<int>& nums) {
    vector<bool> visited(nums.size());
    for (int a : nums) {
        if (visited[a]) {
            return a;
        }
        visited[a] = true;
    }
    return 0;
}
int main() {
    vector<int> nums{1,3,4,2,2};
    cout << findDuplicate(nums) << endl;
    nums = {3,1,3,4,2};
    cout << findDuplicate(nums) << endl;
}

Output:
2
3

Complexity

• Runtime: O(N), where N = nums.length.

• Extra space: O(logN). std::vector<bool> is optimized for space-efficient.

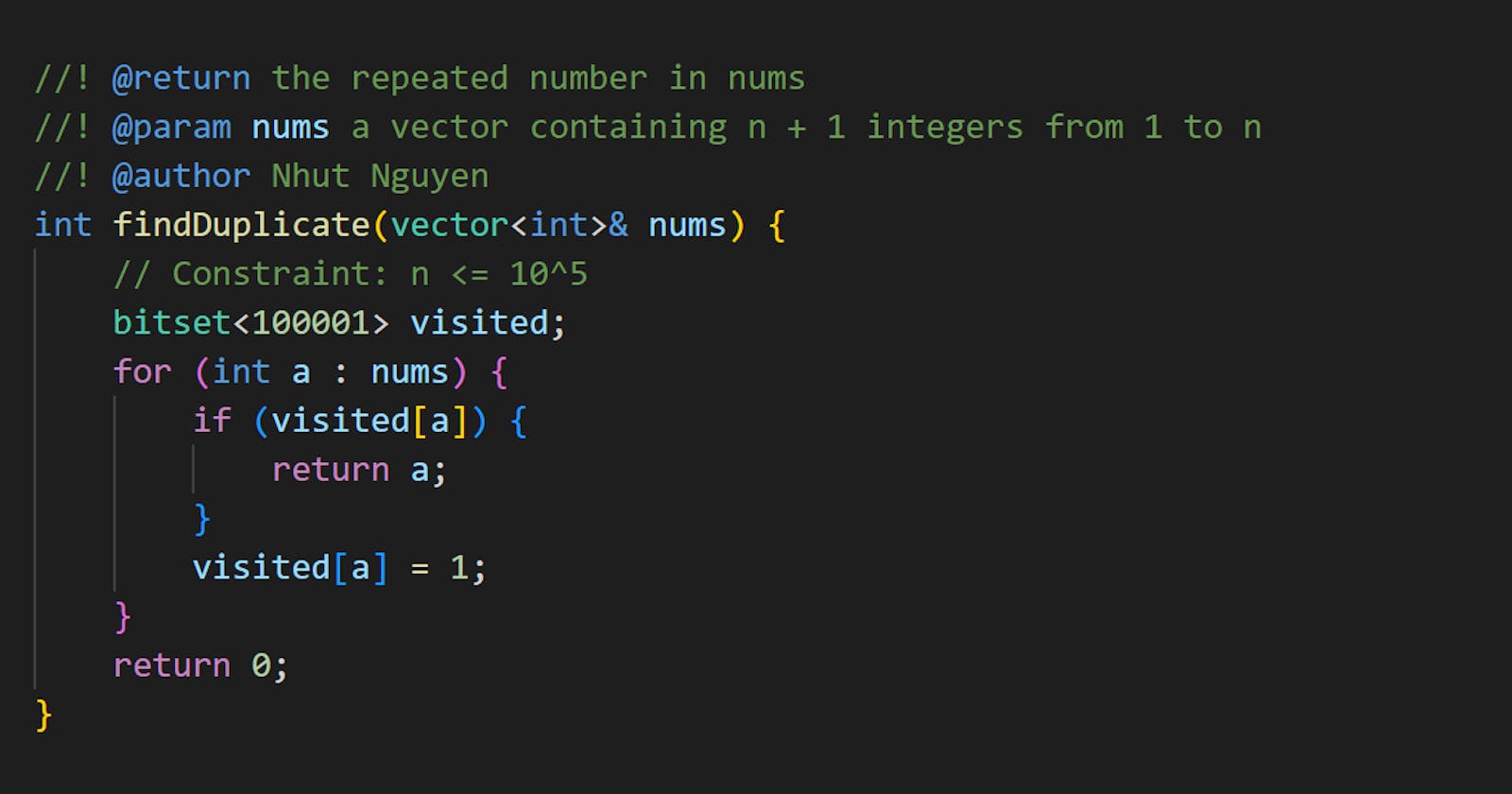
Solution 3: Marking with std::bitset

Since n <= 10^5, you can use this size for a std::bitset to do the marking.

Code

#include <vector>
#include <iostream>
#include <bitset>
using namespace std;
int findDuplicate(vector<int>& nums) {
    bitset<100001> visited;
    for (int a : nums) {
        if (visited[a]) {
            return a;
        }
        visited[a] = 1;
    }
    return 0;
}
int main() {
    vector<int> nums{1,3,4,2,2};
    cout << findDuplicate(nums) << endl;
    nums = {3,1,3,4,2};
    cout << findDuplicate(nums) << endl;
}

Output:
2
3

Complexity

• Runtime: O(N), where N = nums.length.

• Extra space: O(1).

References

• https://leetcode.com/problems/find-the-duplicate-number/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.