Problem statement

You are given an array target of n integers. From a starting array arr consisting of n 1's, you may perform the following procedure:

• Let x be the sum of all elements currently in your array arr.

• Choose any index i such that 0 <= i < n and set the value arr[i] = x.

• You may repeat this procedure as many times as needed.

Return true if it is possible to construct the target array from arr, otherwise, return false.

Example 1

Input: target = [9,3,5]
Output: true
Explanation: Start with arr = [1, 1, 1] 
[1, 1, 1], sum = 3 choose index 1
[1, 3, 1], sum = 5 choose index 2
[1, 3, 5], sum = 9 choose index 0
[9, 3, 5] Done

Example 2

Input: target = [1,1,1,2]
Output: false
Explanation: Impossible to create target array from [1,1,1,1].

Example 3

Input: target = [8,5]
Output: true

Constraints

• n == target.length.

• 1 <= n <= 5 * 10^4.

• 1 <= target[i] <= 10^9.

Solution 1: Going backward

If you start from arr = [1,1,...,1] and follow the required procedure, the new element x you get for the next state is always the max element of arr.

To solve this problem, you can start from the max element of the given target to compute its previous state until you get the arr = [1,1,...,1].

Example 1

For target = [9,3,5]:

• The max element is 9, subtract it from the remaining sum: 9 - (3 + 5) = 1, you get target = [1,3,5].

• The max element is 5, subtract it from the remaining sum: 5 - (1 + 3) = 1, you get target = [1,3,1].

• The max element is 3, subtract it from the remaining sum: 3 - (1 + 1) = 1, you get target = [1,1,1].

• Return true.

Notes

• If target = [m,1] or target = [1,m] for any m >= 1, you can always turn it to arr = [1,1].

• If the changed value after the subtraction is still the max element of the previous state, you need to redo the subtraction at the same position. In this case, the modulo might be used instead of subtraction.

Code

#include <iostream>
#include <numeric>
#include <algorithm>
#include <vector>
using namespace std;
bool isPossible(vector<int>& target) {
    unsigned long sum = accumulate(target.begin(), target.end(), (unsigned long) 0);
    auto pmax = max_element(target.begin(), target.end());
    while (*pmax > 1) {
        sum -= *pmax;
        if (sum == 1) {
            // This is the case target = [m,1], which you can always turn it to [1,1].
            return true;
        }
        if (*pmax <= sum) {
            return false;
        }
        if (sum == 0) {
            return false;
        }
        *pmax %= sum;
        if (*pmax == 0) {
            return false;
        }
        sum += *pmax;
        pmax = max_element(target.begin(), target.end());
    }
    return sum == target.size();
}
int main() {
    vector<int> target{9,3,5};
    cout << isPossible(target) << endl;
    target = {1,1,1,2};
    cout << isPossible(target) << endl;
    target = {8,5};
    cout << isPossible(target) << endl;
}

Output:
1
0
1

Complexity

• Runtime: O(logN), where N = max(target).

• Extra space: O(1).

Solution 2: Using priority_queue

In the solution above, the position of the max element in each state is not so important as long as you update exactly it, not the other ones.

That might lead to the usage of the std::priority_queue.

Code

#include <iostream>
#include <numeric>
#include <queue>
#include <vector>
using namespace std;
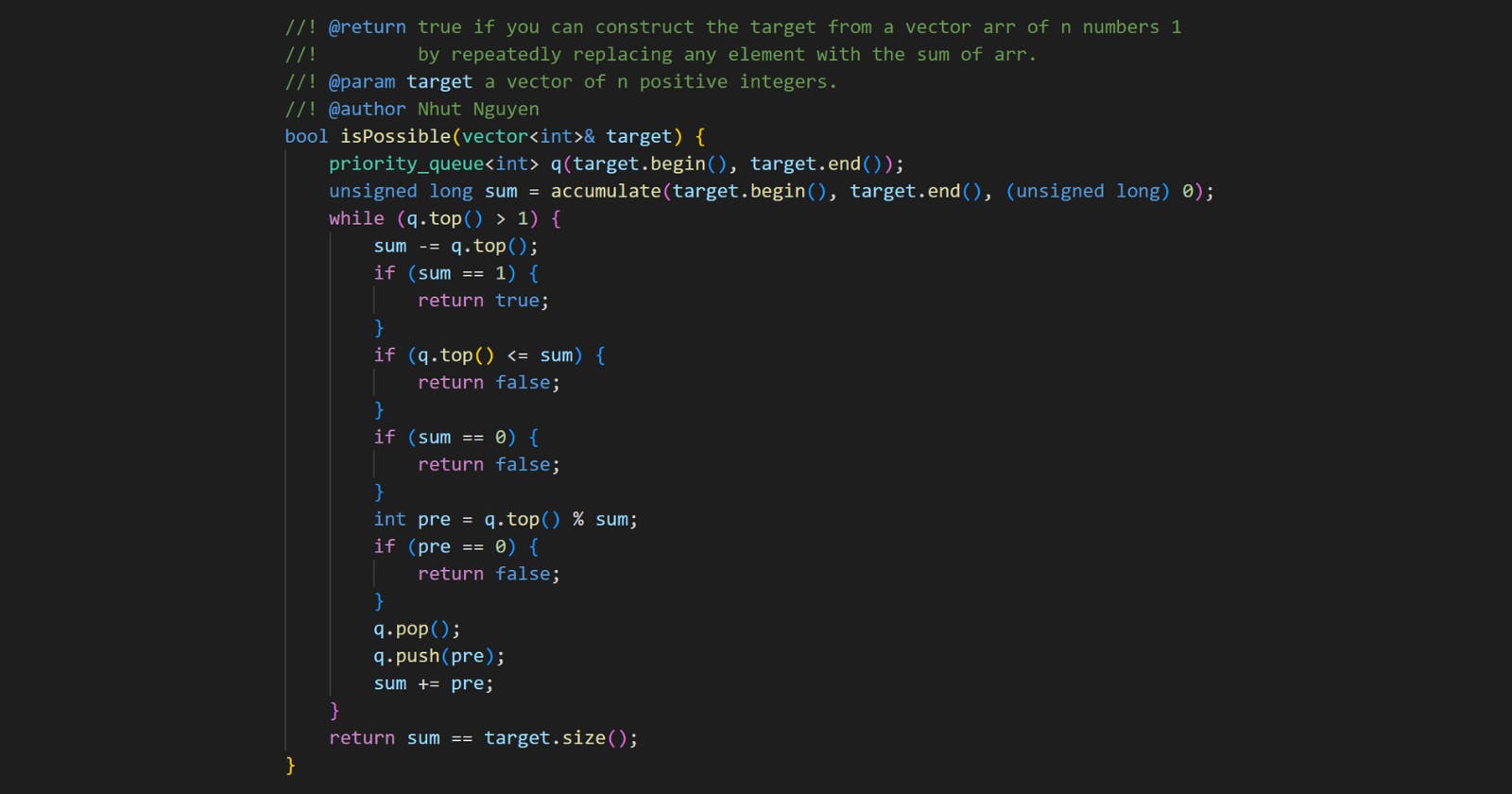
bool isPossible(vector<int>& target) {
    priority_queue<int> q(target.begin(), target.end());
    unsigned long sum = accumulate(target.begin(), target.end(), (unsigned long) 0);
    while (q.top() > 1) {
        sum -= q.top();
        if (sum == 1) {
            return true;
        }
        if (q.top() <= sum) {
            return false;
        }
        if (sum == 0) {
            return false;
        }
        int pre = q.top() % sum;
        if (pre == 0) {
            return false;
        }
        q.pop();
        q.push(pre);
        sum += pre;
    }
    return sum == target.size();
}
int main() {
    vector<int> target{9,3,5};
    cout << isPossible(target) << endl;
    target = {1,1,1,2};
    cout << isPossible(target) << endl;
    target = {8,5};
    cout << isPossible(target) << endl;
}

Output:
1
0
1

Complexity

• Runtime: O(logN), where N = max(target).

• Extra space: O(n), where n = target.length.

References

• https://leetcode.com/problems/construct-target-array-with-multiple-sums/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.