Problem statement

Given a 2D grid of size m x n and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] moves to grid[i][j + 1].

• Element at grid[i][n - 1] moves to grid[i + 1][0].

• Element at grid[m - 1][n - 1] moves to grid[0][0].

Return the 2D grid after applying shift operation k times.

Example 1

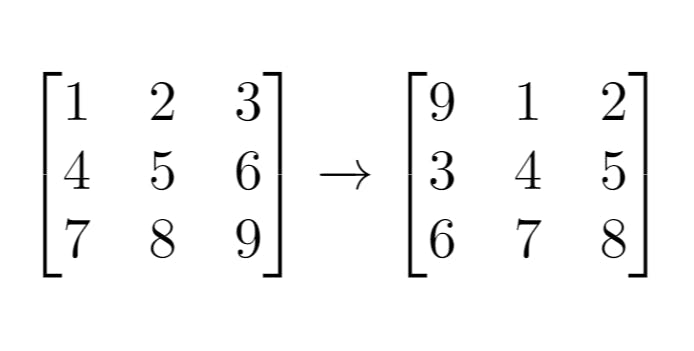
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2

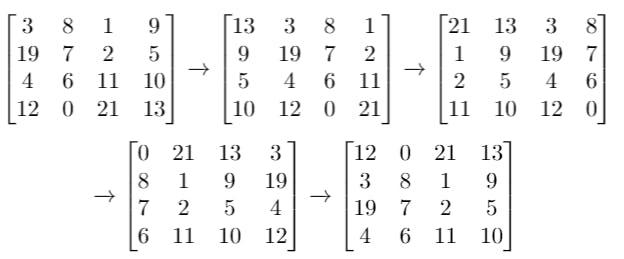
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

Constraints

• m == grid.length.

• n == grid[i].length.

• 1 <= m <= 50.

• 1 <= n <= 50.

• -1000 <= grid[i][j] <= 1000.

• 0 <= k <= 100.

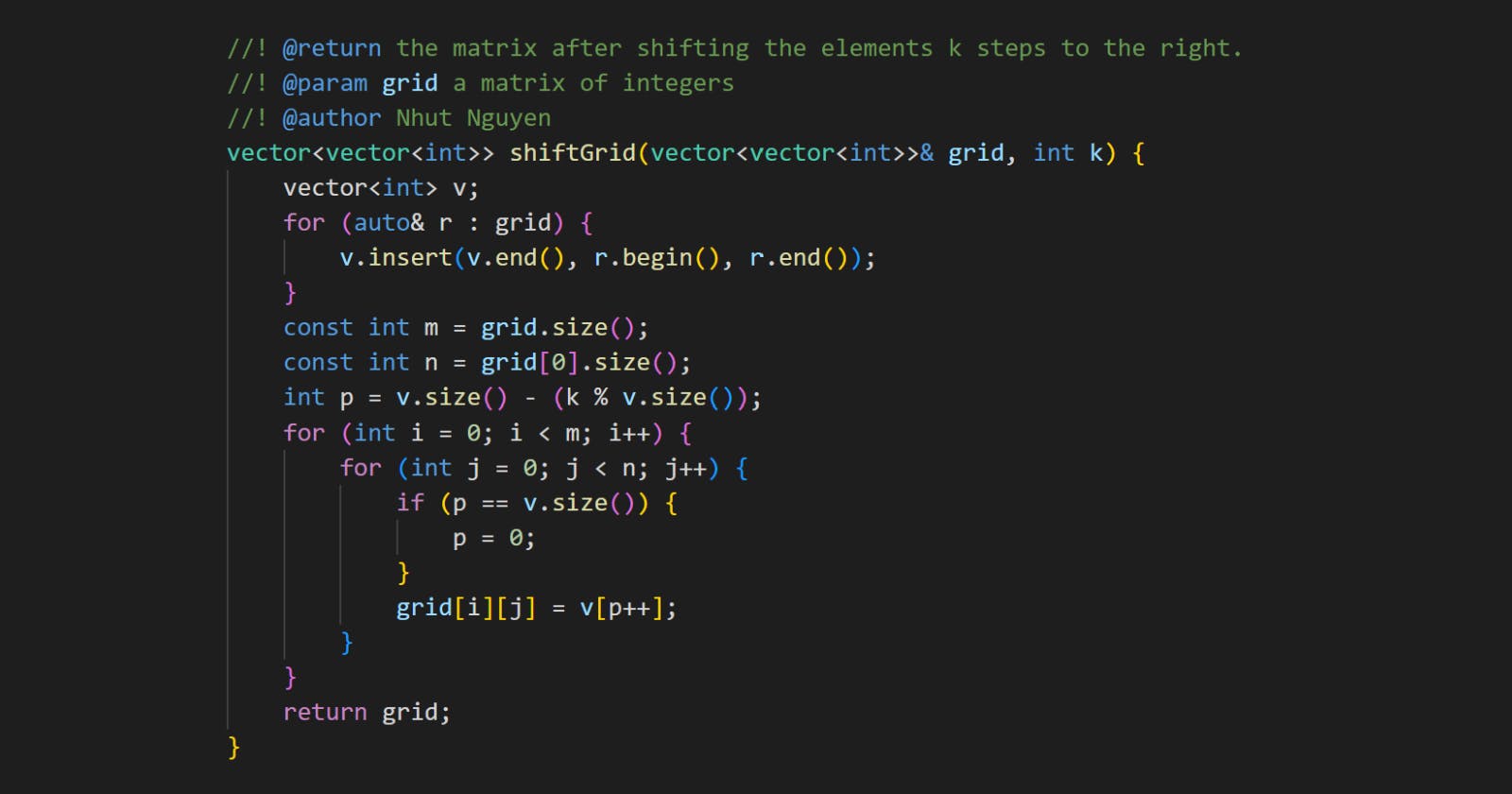
Solution: Convert a 2D array into an 1D one

You can convert the 2D grid into a 1D vector v to perform the shifting easier. One way of doing this is concatenating the rows of the matrix.

• If you shift the grid k = i*N times where N = v.size() and i is any non-negative integer, you go back to the original grid; i.e. you did not shift it.

• If you shift the grid k times with 0 < k < N, the first element of the result starts from v[N - k].

• In general, the first element of the result starts from v[N - k%N].

Example 1

For grid = [[1,2,3],[4,5,6],[7,8,9]]:

• It can be converted into a 1D vector v = [1,2,3,4,5,6,7,8,9] of size m*n = 9.

• With k = 1 the shifted grid now starts from v[9 - 1] = 9.

• The final result is grid = [[9,1,2][3,4,5][6,7,8]].

Code

#include <vector>
#include <iostream>
using namespace std;
vector<vector<int>> shiftGrid(vector<vector<int>>& grid, int k) {
    vector<int> v;
    for (auto& r : grid) {
        v.insert(v.end(), r.begin(), r.end());
    }
    const int m = grid.size();
    const int n = grid[0].size();
    int p = v.size() - (k % v.size());
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if (p == v.size()) {
                p = 0;
            }
            grid[i][j] = v[p++];
        }
    }
    return grid;
}
void printResult(vector<vector<int>>& grid) {
    cout << "[";
    for (auto& r : grid) {
        cout << "[";
        for (int a: r) {
            cout << a << ",";
        }
        cout << "]";
    }
    cout << "]\n";
}
int main() {
    vector<vector<int>> grid{{1,2,3},{4,5,6},{7,8,9}};
    auto result = shiftGrid(grid, 1);
    printResult(result);
    grid = {{3,8,1,9},{19,7,2,5},{4,6,11,10},{12,0,21,13}};
    result = shiftGrid(grid, 4);
    printResult(result);
    grid = {{1,2,3},{4,5,6},{7,8,9}};
    result = shiftGrid(grid, 9);
    printResult(result);
}

Output:
[[9,1,2,][3,4,5,][6,7,8,]]
[[12,0,21,13,][3,8,1,9,][19,7,2,5,][4,6,11,10,]]
[[1,2,3,][4,5,6,][7,8,9,]]

Complexity

• Runtime: O(mn) (the nested for loops), where m = grid.length, n = grid[i].length.

• Extra space: O(mn) (the vector v).

C++ notes

1. To convert a 2D matrix into a 1D vector, you can use the vector's function insert().

2. The modulo operator % is usually used to index an array to ensure the index is inbound.

---

Thanks for reading. Feel free to share your thought about my content.

What is your approach? The problem was picked from leetcode.com. You can submit your solution in any programming language and check the performance.