Problem statement

You are given an array of integers stones where stones[i] is the weight of the i-th stone.

We are playing a game with the stones. On each turn, we choose the heaviest two stones and smash them together. Suppose the heaviest two stones have weights x and y with x <= y. The result of this smash is:

• If x == y, both stones are destroyed, and

• If x != y, the stone of weight x is destroyed, and the stone of weight y has new weight y - x.

At the end of the game, there is at most one stone left.

Return the smallest possible weight of the left stone. If there are no stones left, return 0.

Example 1

Input: stones = [2,7,4,1,8,1]
Output: 1
Explanation: 
We combine 7 and 8 to get 1, so the array converts to [2,4,1,1,1] then,
we combine 2 and 4 to get 2, so the array converts to [2,1,1,1] then,
we combine 2 and 1 to get 1, so the array converts to [1,1,1] then,
we combine 1 and 1 to get 0, so the array converts to [1] then that's the value of the last stone.

Example 2

Input: stones = [1]
Output: 1

Constraints

• 1 <= stones.length <= 30.

• 1 <= stones[i] <= 1000.

Solution: Keeping the heaviest stones on top

The only things you want at any time are the two heaviest stones. One way of keeping this condition is by using std::priority_queue.

Code

#include <vector>
#include <iostream>
#include <queue>
using namespace std;
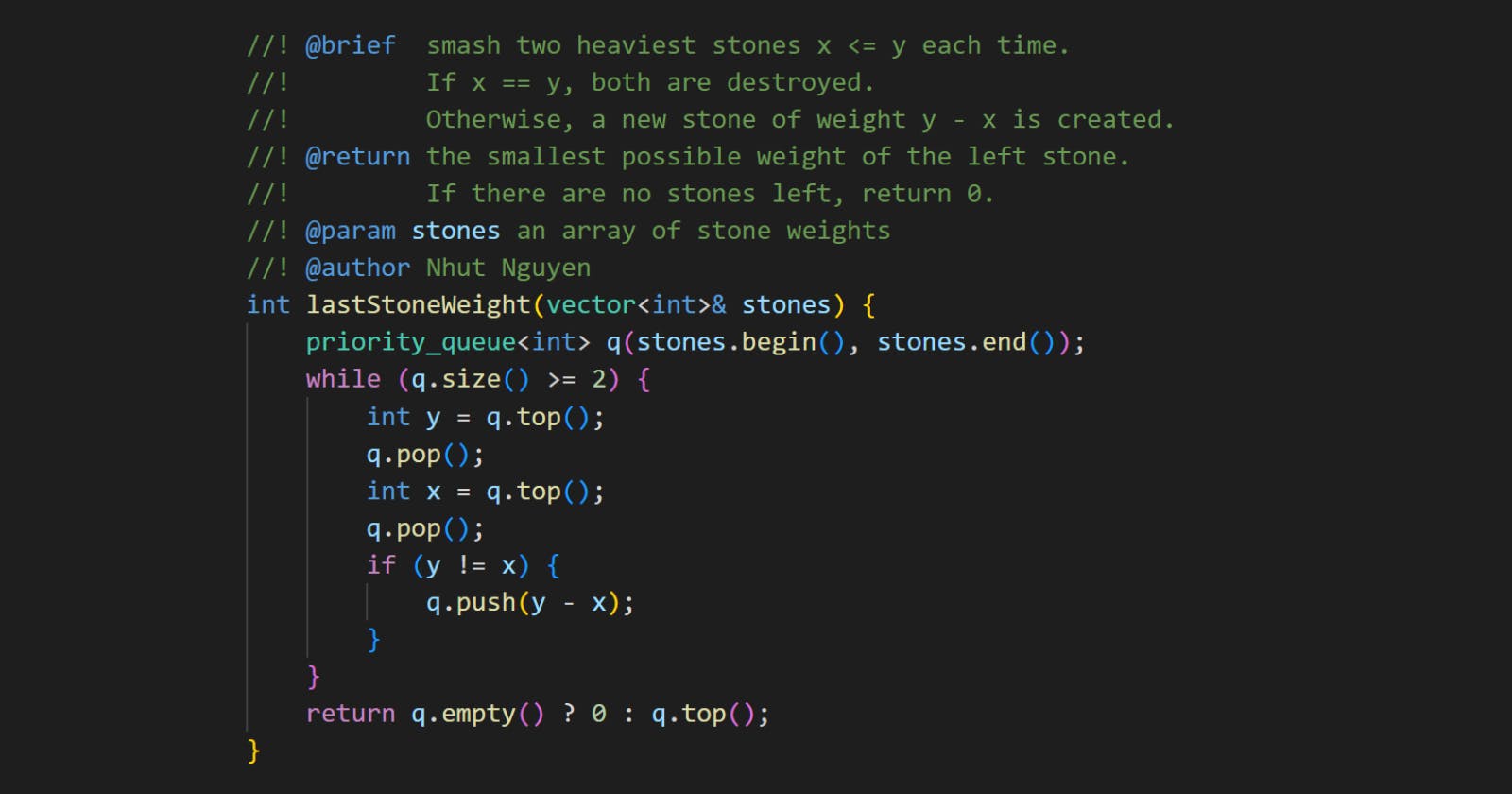
int lastStoneWeight(vector<int>& stones) {
    priority_queue<int> q(stones.begin(), stones.end());
    while (q.size() >= 2) {
        int y = q.top();
        q.pop();
        int x = q.top();
        q.pop();
        if (y != x) {
            q.push(y - x);
        }
    }
    return q.empty() ? 0 : q.top();    
}
int main() {
    vector<int> stones{2,7,4,1,8,1};
    cout << lastStoneWeight(stones) << endl;
    stones = {1};
    cout << lastStoneWeight(stones) << endl;
}

Output:
1
1

Complexity

• Runtime: worst case O(NlogN), on average O(N), where N = stones.length.

• Extra space: O(N).

References

• https://leetcode.com/problems/last-stone-weight/

Thanks for reading. Feel free to share your thought about my content and check out my FREE book “10 Classic Coding Challenges”.